题目内容
20.下列各组函数f(x)与g(x)的图象相同的是( )| A. | f(x)=(x-1)0与g(x)=1 | B. | f(x)=x与g(x)=$\sqrt{x^2}$ | ||
| C. | f(x)=$\frac{{{x^2}-4}}{x-2}$,g(x)=x+2 | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}x(x≥0)\\-x(x<0)\end{array}$ |
分析 分别判断两个函数的定义域和对应法则是否相同即可.
解答 解:A.f(x)=(x-1)0的定义域为{x|x≠1},两个函数的定义域不同,不是同一函数.
B.g(x)=$\sqrt{x^2}$=|x|,两个函数的对应法则不同,不是同一函数.
C.f(x)=$\frac{{{x^2}-4}}{x-2}$=x+2,定义域为{x|x≠2},两个函数的定义域不同,不是同一函数.
D.f(x)=|x|=$\left\{\begin{array}{l}x(x≥0)\\-x(x<0)\end{array}$,两个函数的定义域和对应法则相同是同一函数,
故选:D
点评 本题主要考查判断两个函数是否为同一函数,判断的标准就是判断两个函数的定义域和对应法则是否一致,否则不是同一函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
通过计算得到回归方程为$\stackrel{∧}{y}$=0.577x-0.448,利用这个方程,我们得到年龄37岁时体内脂肪含量为20.90%,那么数据20.90%的意义是( )
| 年龄 | 23 | 27 | 39 | 41 | 45 | 49 | 50 | 53 | 56 | 58 | 60 |
| 脂肪 | 9.5 | 17.8 | 21.2 | 25.9 | 27.5 | 26.3 | 28.2 | 29.6 | 31.4 | 33.5 | 35.2 |
| A. | 某人年龄37岁,他体内脂肪含量为20.90% | |
| B. | 某人年龄37岁,他体内脂肪含量为20.90%的概率最大 | |
| C. | 某人年龄37岁,他体内脂肪含量的期望值为20.90% | |
| D. | 20.90%是对年龄为37岁的人群中的大部分人的体内脂肪含量所作出的估计 |
11.设集合M={1,3},N={1,2,3},则M∪N=( )
| A. | {2} | B. | {1,2} | C. | {1,3} | D. | {1,2,3} |
8.阅读如图的程序框图.若输入n=1,则输出k的值为( )
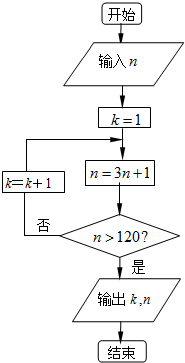

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
15.把座位编号为1,2,3,4,5,6的6张电影票分给甲、乙、丙、丁四个人,每人至少分一张,至多分两张,且分得的两张票必须是连号,那么不同分法种数为( )
| A. | 240 | B. | 144 | C. | 196 | D. | 288 |
12.把函数y=sinx的图象上所有点向右平移$\frac{π}{3}$个单位,再将图象上所有点的横坐标缩小到原来的$\frac{1}{2}$(纵坐标不变),所得函数解析式为y=sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<0),则( )
| A. | ω=2,φ=-$\frac{π}{3}$ | B. | ω=2,φ=-$\frac{π}{6}$ | C. | ω=$\frac{1}{2},φ=-\frac{π}{6}$ | D. | ω=$\frac{1}{2},φ=-\frac{π}{3}$ |