题目内容
某大学的四位学生参加了志愿者活动,他们从甲、乙、丙三个比赛项目中,任选一项进行志愿者服务,每个项目允许有多人服务,假设每位学生选择哪项是等可能的.
(1)求这四位学生中至少有一位选择甲项目的概率;
(2)用随机变量ξ表示四位学生选择丙项目的人数,求其分布列和数学期望.
(1)求这四位学生中至少有一位选择甲项目的概率;
(2)用随机变量ξ表示四位学生选择丙项目的人数,求其分布列和数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:应用题,概率与统计
分析:(1)利用对立事件,即可求得结论;
(2)确定随机变量ξ的可能取值,求出相应的概率,即可得到随机变量ξ的分布列和数学期望.
(2)确定随机变量ξ的可能取值,求出相应的概率,即可得到随机变量ξ的分布列和数学期望.
解答:
解:(1)由题意,四位学生中至少有一位选择甲项目的概率为1-
=
;
(2)随机变量ξ=0,1,2,3,4,则
P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=3)=
=
,P(ξ=4)=
,
ξ的分布列为
Eξ=0×
+1×
+2×
+3×
+4×
=
| 24 |
| 34 |
| 65 |
| 81 |
(2)随机变量ξ=0,1,2,3,4,则
P(ξ=0)=
| 24 |
| 34 |
| 16 |
| 81 |
| 4×23 |
| 34 |
| 32 |
| 81 |
| ||
| 34 |
| 24 |
| 81 |
| ||
| 34 |
| 8 |
| 81 |
| 1 |
| 81 |
ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 16 |
| 81 |
| 32 |
| 81 |
| 24 |
| 81 |
| 8 |
| 81 |
| 1 |
| 81 |
| 4 |
| 3 |
点评:本题考查概率的计算,考查离散型随机变量的分布列与数学期望,正确求概率是关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
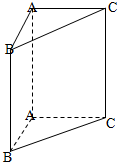 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=