题目内容
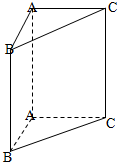 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=| 3 |
(1)证明:AB⊥A1C;
(2)求二面角A-A1C-B的大小.
考点:二面角的平面角及求法
专题:综合题,空间位置关系与距离,空间角
分析:(1)欲证AB⊥A1C,而A1C?平面ACC1A1,可先证AB⊥平面ACC1A1,根据三棱柱ABC-A1B1C1为直三棱柱,可知AB⊥AA1,由正弦定理得AB⊥AC,满足线面垂直的判定定理所需条件;
(2)作AD⊥A1C交A1C于D点,连接BD,由三垂线定理知BD⊥A1C,则∠ADB为二面角A-A1C-B的平面角,在Rt△BAD中,求出二面角A-A1C-B的余弦值即可.
(2)作AD⊥A1C交A1C于D点,连接BD,由三垂线定理知BD⊥A1C,则∠ADB为二面角A-A1C-B的平面角,在Rt△BAD中,求出二面角A-A1C-B的余弦值即可.
解答:
 (1)证明:∵三棱柱ABC-A1B1C1为直三棱柱,∴AB⊥AA1,
(1)证明:∵三棱柱ABC-A1B1C1为直三棱柱,∴AB⊥AA1,
在△ABC中,AB=1,AC=
,∠ABC=60°,由正弦定理得∠ACB=30°,
∴∠BAC=90°,即AB⊥AC,
∴AB⊥平面ACC1A1,
又A1C?平面ACC1A1,
∴AB⊥A1C.
(2)解:如图,作AD⊥A1C交A1C于D点,连接BD,
由三垂线定理知BD⊥A1C,
∴∠ADB为二面角A-A1C-B的平面角.
在Rt△AA1C中,AD=
=
,
在Rt△BAD中,tan∠ADB=
=
,
∴cos∠ADB=
,
即二面角A-A1C-B的大小为arccos
.
 (1)证明:∵三棱柱ABC-A1B1C1为直三棱柱,∴AB⊥AA1,
(1)证明:∵三棱柱ABC-A1B1C1为直三棱柱,∴AB⊥AA1,在△ABC中,AB=1,AC=
| 3 |
∴∠BAC=90°,即AB⊥AC,
∴AB⊥平面ACC1A1,
又A1C?平面ACC1A1,
∴AB⊥A1C.
(2)解:如图,作AD⊥A1C交A1C于D点,连接BD,
由三垂线定理知BD⊥A1C,
∴∠ADB为二面角A-A1C-B的平面角.
在Rt△AA1C中,AD=
| ||||
|
| ||
| 2 |
在Rt△BAD中,tan∠ADB=
| AB |
| AD |
| ||
| 3 |
∴cos∠ADB=
| ||
| 5 |
即二面角A-A1C-B的大小为arccos
| ||
| 5 |
点评:本题考查直线与平面垂直的性质,二面角及其度量,考查空间想象能力,逻辑思维能力,计算能力,是中档题.

练习册系列答案
相关题目
已知集合M={x|y=-
},集合N={y|y=ex,x∈R}(e是自然对数的底数),则M∩N=( )
| 1-x |
| A、{x|0<x≤1} |
| B、{x|0<x<1} |
| C、{x|0<x<1} |
| D、∅ |
抛物线y2=2px上不同两点A,B(异于原点O)若OA,OB所在直线斜率之和定值m(m≠0)则直线AB必经过( )
A、(0,
| ||
B、(0,
| ||
C、(-
| ||
D、(-
|
若tanα=lg(10a),tanβ=lg(
),且α+β=
,则实数a的值为( )
| 1 |
| a |
| π |
| 4 |
| A、1 | ||
B、
| ||
C、1或
| ||
| D、1或10 |
设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|