题目内容
在平行六面体ABCD-A1B1C1D1中,M、N、P分别是CC1、B1C1、C1D1的中点.求证:∠NMP=∠BA1D.
考点:棱柱的结构特征
专题:证明题,空间位置关系与距离
分析:连接B1D1、B1C,在△B1C1C中,利用中位线定理得到MN∥CB1,再在平行四边形A1B1CD中,A1D∥CB1,所以A1D∥MN,同理,可得PM∥A1B,利用∠NMP与∠BA1D方向相同,即可得出结论.
解答:
证明: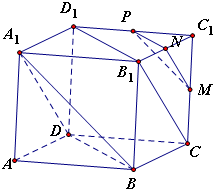 连接B1D1、B1C,
连接B1D1、B1C,
∵正方体AC1中,A1B1∥CD且A1B1=CD
∴四边形A1B1CD是平行四边形,可得A1D∥CB1
又∵△B1C1C中,M、N分别是CC1、B1C1的中点.
∴MN∥CB1
∴A1D∥MN
同理,可得PM∥A1B.
∵∠NMP与∠BA1D方向相同,
∴∠NMP=∠BA1D.
 连接B1D1、B1C,
连接B1D1、B1C,∵正方体AC1中,A1B1∥CD且A1B1=CD
∴四边形A1B1CD是平行四边形,可得A1D∥CB1
又∵△B1C1C中,M、N分别是CC1、B1C1的中点.
∴MN∥CB1
∴A1D∥MN
同理,可得PM∥A1B.
∵∠NMP与∠BA1D方向相同,
∴∠NMP=∠BA1D.
点评:本题给出经过正方体三条棱中点的平面,求证∠NMP=∠BA1D,着重考查了线面平行的判定与性质,属于基础题.

练习册系列答案
相关题目
在椭圆
+
=1(a>b>0)中,F1、F2分别是其左右焦点,若椭圆上存在点P使得|PF1|-2|PF2|=a,则该椭圆的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(
| ||
B、(0,
| ||
C、[
| ||
D、[
|