题目内容
【题目】三棱锥A﹣BCD及其侧视图、俯视图如图所示，设M，N分别为线段AD，AB的中点，P为线段BC上的点，且MN⊥NP．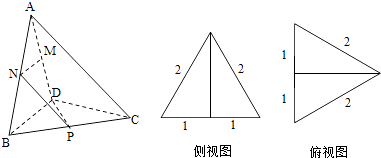 
（1）证明：P是线段BC的中点；
（2）求二面角A﹣NP﹣M的余弦值．
【答案】
（1）证明：由三棱锥A﹣BCD及其侧视图、俯视图可知，在三棱锥A﹣BCD中：
平面ABD⊥平面CBD，AB=AD=BD=CD=CB=2
设O为BD的中点，连接OA，OC
于是OA⊥BD，OC⊥BD 所以BD⊥平面OACBD⊥AC
因为M，N分别为线段AD，AB的中点，所以MN∥BD，MN⊥NP，故BD⊥NP
假设P不是线段BC的中点，则直线NP与直线AC是平面ABC内相交直线
从而BD⊥平面ABC，这与∠DBC=60°矛盾，所以P为线段BC的中点
（2）解：以O为坐标原点，OB，OC，OA分别为x，y，z轴建立空间直角坐标系，
则A（0，0， 
），M（ 
，O， 
），N（ 
，0， 
），P（ ， ，0）
于是 
， 
， 
设平面ANP和平面NPM的法向量分别为 
和 
由 
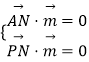，则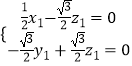 
，设z1=1，则 
由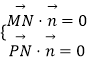 
，则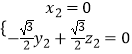 
，设z2=1，则 
cos 
= 
= 
= 
所以二面角A﹣NP﹣M的余弦值
【解析】（1）用线面垂直的性质和反证法推出结论，（2）先建空间直角坐标系，再求平面的法向量，即可求出二面角A﹣NP﹣M的余弦值．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
【题目】在一次抽样调查中测得样本的6组数据，得到一个变量
关于
的回归方程模型，其对应的数值如下表：
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)请用相关系数
加以说明与之间存在线性相关关系(当
时，说明与之间具有线性相关关系)；
(2)根据(1)的判断结果，建立关于的回归方程并预测当
时，对应的值为多少(
精确到
).
附参考公式：回归方程
中斜率和截距的最小二乘法估计公式分别为：
，
，相关系数公式为：
.
参考数据：
，
，
，
.
