题目内容
【题目】已知![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 是
是![]() 展开式中所有无理项的二项式系数和,数列
展开式中所有无理项的二项式系数和,数列![]() 是各项都大于1的数组成的数列,试用数学归纳法证明:
是各项都大于1的数组成的数列,试用数学归纳法证明:![]() .
.
【答案】(1)![]() . (2)165.(3)见解析.
. (2)165.(3)见解析.
【解析】分析:(1)求得![]() ,可得
,可得![]() ;(2)由二项展开式定理可得
;(2)由二项展开式定理可得![]()
![]() ;(3)因为
;(3)因为![]() ,为无理项,所以
,为无理项,所以![]() 必为奇数,所以
必为奇数,所以![]() ,利用数学归纳法证明即可.
,利用数学归纳法证明即可.
详解:(1)由题意![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)![]() ,
,
所以![]()
![]() .
.
(3)因为![]() ,所以要得无理项,
,所以要得无理项,![]() 必为奇数,
必为奇数,
所以![]() ,
,
要证明![]() ,
,
只要证明![]() ,用数学归纳法证明如下:
,用数学归纳法证明如下:
(Ⅰ)当![]() 时,左边=右边,
时,左边=右边,
当![]() 时,
时,![]() ,
,
∴![]() 时,不等式成立.
时,不等式成立.
(Ⅱ)假设当![]()
![]() 时,
时,![]() 成立,
成立,
则![]() 时,
时,![]() (*)
(*)
∵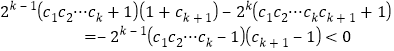 ,
,
∴结合(*)得:![]() 成立,
成立,
∴![]() 时,不等式成立.
时,不等式成立.
综合(Ⅰ)(Ⅱ)可知![]() 对一切
对一切![]() 均成立.
均成立.
∴不等式![]() 成立 .
成立 .

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目