题目内容
【题目】记max{x,y}= ![]() ,min{x,y}=
,min{x,y}= ![]() ,设
,设 ![]() ,
, ![]() 为平面向量,则( )
为平面向量,则( )
A.min{| ![]() +
+ ![]() |,|
|,| ![]() ﹣
﹣ ![]() |}≤min{|
|}≤min{| ![]() |,|
|,| ![]() |}
|}
B.min{| ![]() +
+ ![]() |,|
|,| ![]() ﹣
﹣ ![]() |}≥min{|
|}≥min{| ![]() |,|
|,| ![]() |}
|}
C.max{| ![]() +
+ ![]() |2 , |
|2 , | ![]() ﹣
﹣ ![]() |2}≤|
|2}≤| ![]() |2+|
|2+| ![]() |2
|2
D.max{| ![]() +
+ ![]() |2 , |
|2 , | ![]() ﹣
﹣ ![]() |2}≥|
|2}≥| ![]() |2
|2
【答案】D
【解析】解:对于选项A,取 ![]() ⊥
⊥ ![]() ,则由图形可知,根据勾股定理,结论不成立;
,则由图形可知,根据勾股定理,结论不成立;
对于选项B,取 ![]() ,
, ![]() 是非零的相等向量,则不等式左边min{|
是非零的相等向量,则不等式左边min{| ![]() +
+ ![]() |,|
|,| ![]() ﹣
﹣ ![]() |}=0,显然,不等式不成立;
|}=0,显然,不等式不成立;
对于选项C,取 ![]() ,
, ![]() 是非零的相等向量,则不等式左边max{|
是非零的相等向量,则不等式左边max{| ![]() +
+ ![]() |2 , |
|2 , | ![]() ﹣
﹣ ![]() |2}=|
|2}=| ![]() +
+ ![]() |2=4
|2=4 ![]() ,而不等式右边=|
,而不等式右边=| ![]() |2+|
|2+| ![]() |2=2
|2=2 ![]() ,故C不成立,D选项正确.
,故C不成立,D选项正确.
故选:D.
将 ![]() ,
, ![]() 平移到同一起点,根据向量加减法的几何意义可知,
平移到同一起点,根据向量加减法的几何意义可知, ![]() +
+ ![]() 和
和 ![]() ﹣
﹣ ![]() 分别表示以
分别表示以 ![]() ,
, ![]() 为邻边所做平行四边形的两条对角线,再根据选项内容逐一判断.
为邻边所做平行四边形的两条对角线,再根据选项内容逐一判断.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
【题目】某二手车交易市场对某型号的二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求![]() 关于
关于![]() 的回归直线方程:(参考公式:
的回归直线方程:(参考公式: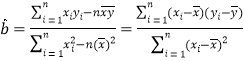 ,
, ![]() .)
.)
(2)已知每辆该型号汽车的收购价格为![]() 万元,根据(1)中所求的回归方程,预测
万元,根据(1)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?
最大?