题目内容
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).在以坐标原点为极点,
).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() .
.
(1)说明![]() 是哪种曲线,并将
是哪种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)已知![]() 与
与![]() 的交于
的交于![]() ,
,![]() 两点,且
两点,且![]() 过极点,求线段
过极点,求线段![]() 的长.
的长.
【答案】(Ⅰ)![]() 为以
为以![]() 为圆心,以
为圆心,以![]() 为半径的圆;
为半径的圆;![]()
(Ⅱ)![]()
【解析】
试题分析:
(1)为知![]() 是哪种曲线,需将
是哪种曲线,需将![]() 的参数方程化为普通方程,再将普通方程化为极坐标方程.(2)先将
的参数方程化为普通方程,再将普通方程化为极坐标方程.(2)先将![]() 与
与![]() 方程化为普通方程,易知AB为
方程化为普通方程,易知AB为![]() 与
与![]() 的公共弦长,在求出弦AB的方程后,由点到直线的距离公式求出C2(0,1)到公共弦的距离为
的公共弦长,在求出弦AB的方程后,由点到直线的距离公式求出C2(0,1)到公共弦的距离为![]() ,由勾股定理即可求出
,由勾股定理即可求出![]()
试题解析:
解:(1)∵曲线C1的参数方程为![]() (t为参数,a>0).
(t为参数,a>0).
∴C1的普通方程为![]() ,
,
∴C1为以C1(![]() ,0)为圆心,以a为半径的圆,
,0)为圆心,以a为半径的圆,
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,得C1的极坐标方程为![]() .
.
(2)解法一:∵曲线![]() .
.
∴![]() ,
,
二者相减得公共弦方程为![]() ,
,
∵AB过极点,∴公共弦方程![]() 过原点,
过原点,
∵a>0,∴a=3,∴公共弦方程为![]() ,
,
则C2(0,1)到公共弦的距离为![]() .
.
∴![]() .
.
解法二:∵AB:θ=θ0,
∴![]() 与ρ2=2ρsinθ+6为ρ的同解方程,
与ρ2=2ρsinθ+6为ρ的同解方程,
∴![]() 或θ=
或θ=![]() .
.
∴![]() .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】新高考3+3最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关决定从某学校高一年级的650名学生中随机抽取男生、女生各25人进行模拟选科经统计,选择全理的人数比不选全理的人数多10人
(1)请完成下面的2×2列联表;
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由.
附: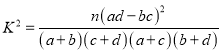 ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |