题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 存在两个极值,求
存在两个极值,求![]() 的取值范围;并证明:函数
的取值范围;并证明:函数![]() 存在唯一零点.
存在唯一零点.
(2)若存在实数![]() ,
,![]() ,使
,使![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;证明见解析;(2)
;证明见解析;(2) ![]()
【解析】
(1)求出![]() 的导数,结合二次函数的性质得到关于
的导数,结合二次函数的性质得到关于![]() 的不等式组,解出即得
的不等式组,解出即得![]() 的范围;令
的范围;令
![]() ,求出
,求出 ,得到
,得到![]() 至多有一个零点,再验证
至多有一个零点,再验证![]() ,即可证明;
,即可证明;
(2)求出![]() ,以及
,以及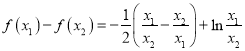 ,设
,设![]() ,记
,记![]() ,根据导数与单调性,最值的应用,即可求解.
,根据导数与单调性,最值的应用,即可求解.
由题意![]() ,
,
所以方程![]() 有两个不相等的正实数根
有两个不相等的正实数根![]() ,不妨设
,不妨设![]() ,则
,则
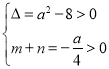 ,解得:
,解得:![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() ;
;
由题易知![]() 在
在![]() 处取得极大值,当
处取得极大值,当![]() 处取得极小值,且有
处取得极小值,且有
![]() ,故
,故![]() ,
,
令![]() ,故
,故![]() ,
,
令![]() ,解得
,解得![]() ,
,
由导数与函数的最值可知:
故![]() ,所以
,所以![]() 至多有一个零点,
至多有一个零点,
又因![]() ,
,
所以函数![]() 存在唯一零点;
存在唯一零点;
由题意知:![]() ,
,
即![]() ,
,
故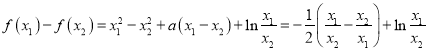 ,
,
设![]() ,记
,记![]()
则![]() ,
,
所以![]() 在定义域上单调递减,所以
在定义域上单调递减,所以![]() ,
,
即![]() ,
,
故![]() 的取值范围.为
的取值范围.为![]() .
.

练习册系列答案
相关题目