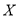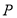题目内容
4. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.(Ⅰ)求椭圆C的方程;
(Ⅱ)直线l:y=k(x-1)(k<0)与椭圆Γ相交于A,B两点.点P(3,0),记直线PA,PB的斜率分别为k1,k2,当$\frac{{k}_{1}{k}_{2}}{k}$最大时,求直线l的方程.
分析 (Ⅰ)由椭圆的离心率为$\frac{\sqrt{2}}{2}$、点G在椭圆上、$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0及△GF1F2的面积为2列式求得a2=4,b2=2,则椭圆方程可求;
(Ⅱ)联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系得到A,B两点横坐标的和与积,把$\frac{{k}_{1}{k}_{2}}{k}$转化为含有k的代数式,利用基本不等式求得使$\frac{{k}_{1}{k}_{2}}{k}$取得最大值的k,则直线Γ的方程可求.
解答 解:(Ⅰ)∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,
∴e=$\frac{c}{a}=\frac{\sqrt{2}}{2}$,①
∵左右焦点分别为F1、F2,点G在椭圆上,
∴|$\overrightarrow{G{F}_{1}}$|+|$\overrightarrow{G{F}_{2}}$|=2a,②
∵$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2,
∴|$\overrightarrow{G{F}_{1}}$|2+|$\overrightarrow{G{F}_{2}}$|2=4c2,③
$\frac{1}{2}|\overrightarrow{G{F}_{1}}|•|\overrightarrow{G{F}_{2}}|=2$,④
联立①②③④,得a2=4,b2=2,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;
(Ⅱ)联立$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,得(1+2k2)x2-4k2x+2k2-4=0.
设A(x1,y1),B(x2,y2),
∴${x}_{1}+{x}_{2}=\frac{4{k}^{2}}{1+2{k}^{2}},{x}_{1}{x}_{2}=\frac{2{k}^{2}-4}{1+2{k}^{2}}$.
$\frac{{k}_{1}{k}_{2}}{k}=\frac{{y}_{1}{y}_{2}}{k({x}_{1}-3)({x}_{2}-3)}=\frac{{k}^{2}({x}_{1}-1)({x}_{2}-1)}{k({x}_{1}-3)({x}_{2}-3)}=k\frac{{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})+1}{{x}_{1}{x}_{2}-3({x}_{1}+{x}_{2})+9}$
=$k•\frac{\frac{2{k}^{2}-4}{1+2{k}^{2}}-\frac{4{k}^{2}}{1+2{k}^{2}}+1}{\frac{2{k}^{2}-4}{1+2{k}^{2}}-3•\frac{4{k}^{2}}{1+2{k}^{2}}+9}$=$k•\frac{2{k}^{2}-4-4{k}^{2}+1+2{k}^{2}}{2{k}^{2}-4-12{k}^{2}+9(1+2{k}^{2})}=\frac{-3k}{5+8{k}^{2}}$
=$\frac{3}{(-\frac{5}{k})+(-8k)}≤\frac{3}{4\sqrt{10}}$,当且仅当$k=-\frac{\sqrt{10}}{4}$时,取得最值.
此时l:y=$-\frac{\sqrt{10}}{4}(x-1)$.
点评 本题考查椭圆方程的求法,考查向量在求解圆锥曲线问题中的应用,考查了直线和圆锥曲线间的关系,训练了利用基本不等式求最值,考查了计算能力,是中档题.

 阅读快车系列答案
阅读快车系列答案 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )| A. | 点P到平面QEF的距离 | B. | 三棱锥P-QEF的体积 | ||
| C. | 直线PQ与平面PEF所成的角 | D. | 二面角P-EF-Q的大小 |
在一次篮球定点投篮训练中,规定每人最多投3次.在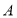 处每投进一球得3分;在
处每投进一球得3分;在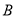 处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在
处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在 处的投中率
处的投中率 ,在
,在 处的投中率为
处的投中率为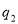 .该同学选择先在
.该同学选择先在 处投一球,以后都在
处投一球,以后都在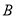 处投,且每次投篮都互不影响.用
处投,且每次投篮都互不影响.用 表示
表示
该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求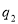 的值;
的值;
(2)求随机变量 的数学期望
的数学期望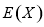 ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.
 4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.
4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.