题目内容
1.已知定点F(3,0)和动点P(x,y),H为PF的中点,O为坐标原点,且满足|OH|-|HF|=2.(1)求点P的轨迹方程;
(2)过点F作直线l与点P的轨迹交于A,B两点,点C(2,0).连接AC,BC与直线x=$\frac{4}{3}$分别交于点M,N.试证明:以MN为直径的圆恒过点F.
分析 (1)取F′(-3,0),连接PF′,可得|PF′|-|PF|=4,由双曲线定义知,点P的轨迹是以F′,F为焦点的双曲线的右支,即可求点P的轨迹方程;
(2)直线l方程为x=ty+3,代入双曲线方程,利用三点共线,求出M,N的坐标,证明$\overrightarrow{FM}$•$\overrightarrow{FN}$=0,即可得出结论.
解答 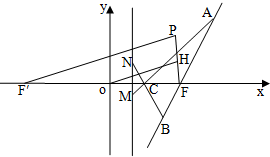 解:(1)如图,取F′(-3,0),连接PF′.
解:(1)如图,取F′(-3,0),连接PF′.
∵|OH|-|HF|=2,
∴|PF′|-|PF|=4
由双曲线定义知,点P的轨迹是以F′,F为焦点的双曲线的右支,
∴a=2,c=3,
∴b=$\sqrt{9-4}$=$\sqrt{5}$
∴P的轨迹方程为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}=1(x>0)$…(5分)
(2)设A(x1,y1),B(x2,y2),M($\frac{4}{3}$,m),N($\frac{4}{3}$,n),
直线l方程为x=ty+3,代入双曲线方程整理得:(5t2-4)y2+30ty+25=0
∴y1+y2=-$\frac{30t}{5{t}^{2}-4}$,y1y2=$\frac{25}{5{t}^{2}-4}$…(6分)
∵A,C,M三点共线,
∴$\frac{{y}_{1}}{{x}_{1}-2}=\frac{m}{\frac{4}{3}-2}$,
∴m=-$\frac{2}{3}$•$\frac{{y}_{1}}{{x}_{1}-2}$
同理n=-$\frac{2}{3}$•$\frac{{y}_{2}}{{x}_{2}-2}$
∴$\overrightarrow{FM}$•$\overrightarrow{FN}$=($\frac{4}{3}$-3,-$\frac{2}{3}$•$\frac{{y}_{1}}{{x}_{1}-2}$)•($\frac{4}{3}$-3,-$\frac{2}{3}$•$\frac{{y}_{2}}{{x}_{2}-2}$)
=$\frac{25}{9}$+$\frac{4}{9}$•$\frac{{y}_{1}{y}_{2}}{{y}_{1}{y}_{2}+t({y}_{1}+{y}_{2})+1}$=$\frac{25}{9}$+$\frac{4}{9}$•$\frac{25}{25{t}^{2}-30{t}^{2}+5{t}^{2}-4}$=0
∴FM⊥FN,
即∠MFN=90°
∴以MN为直径的圆恒过点F…(12分)
点评 本题考查轨迹方程,考查直线与双曲线的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | ${C}_{9}^{3}$ | B. | ${C}_{18}^{3}$ | C. | ${C}_{9}^{4}$ | D. | ${C}_{18}^{6}$ |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.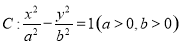 的右焦点为
的右焦点为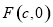 ,直线
,直线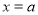 与双曲线
与双曲线 的渐近线在第一象限的交点为
的渐近线在第一象限的交点为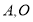 为坐标原点.若
为坐标原点.若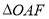 的面积为
的面积为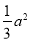 ,则双曲线
,则双曲线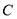 的离心率为( )
的离心率为( )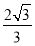 B.
B.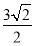
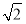 D.
D.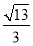
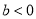 ,且
,且 ,则
,则 等于( )
等于( )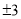 B.-2
B.-2 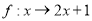 是集合
是集合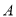 到集合
到集合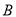 的映射,若
的映射,若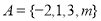 ,
,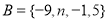 ,则
,则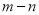 等于( )
等于( )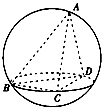 如图,在三棱锥A-BCD中,△ACD与△BCD是全等的等腰三角形,且平面ACD⊥平面BCD,AB=2CD=4,则该三棱锥的外接球的表面积为$\frac{65}{4}π$.
如图,在三棱锥A-BCD中,△ACD与△BCD是全等的等腰三角形,且平面ACD⊥平面BCD,AB=2CD=4,则该三棱锥的外接球的表面积为$\frac{65}{4}π$.