题目内容
16. 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )| A. | 点P到平面QEF的距离 | B. | 三棱锥P-QEF的体积 | ||
| C. | 直线PQ与平面PEF所成的角 | D. | 二面角P-EF-Q的大小 |
分析 根据线面平行的性质可以判断A答案的对错;根据等底同高的三角形面积相等及A的结论结合棱锥的体积公式,可判断B的对错;根据线面角的定义,可以判断C的对错;根据二面角的定义可以判断D的对错,进而得到答案.
解答 解:A中,∵QEF平面也就是平面A1B1CD,既然P和平面QEF都是固定的,∴P到平面QEF的距离是定值.∴点P到平面QEF的距离为定值;
B中,∵△QEF的面积是定值.(∵EF定长,Q到EF的距离就是Q到CD的距离也为定长,即底和高都是定值),
再根据A的结论P到QEF平面的距离也是定值,∴三棱锥的高也是定值,于是体积固定.∴三棱锥P-QEF的体积是定值;
C中,∵Q是动点,EF也是动点,推不出定值的结论,∴就不是定值.∴直线PQ与平面PEF所成的角不是定值;
D中,∵A1B1∥CD,Q为A1B1上任意一点,E、F为CD上任意两点,∴二面角P-EF-Q的大小为定值.
故选:C.
点评 本题考查的知识点是直线与平面所成的角,二面角,棱锥的体积及点到平面的距离,其中两线平行时,一条线的上的点到另一条直线的距离相等,线面平行时直线上到点到平面的距离相等,平面平行时一个平面上的点到另一个平面的距离相等是解答本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
9.过双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1 (a>0,b>0)的一个焦点F向其一条渐近线作垂线l,垂足为A,l与另一条渐近线交于B点,若$\overrightarrow{FB}=2\overrightarrow{FA}$,则双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
7.已知F是抛物线x2=4y的焦点,直线y=kx-1与该抛物线交于第一象限内的零点A,B,若|AF|=3|FB|,则k的值是( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.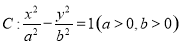 的右焦点为
的右焦点为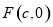 ,直线
,直线 与双曲线
与双曲线 的渐近线在第一象限的交点为
的渐近线在第一象限的交点为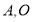 为坐标原点.若
为坐标原点.若 的面积为
的面积为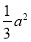 ,则双曲线
,则双曲线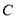 的离心率为( )
的离心率为( ) B.
B.
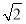 D.
D.