题目内容
12.关于x的分式方程$\frac{x}{x-1}$-2=$\frac{m}{x-1}$无解,则m的值是1.分析 求解分式方程,得到m≠1时方程有解为2-m,由此得到使方程无解的m的值.
解答 解:由$\frac{x}{x-1}$-2=$\frac{m}{x-1}$,得$\frac{2-x}{x-1}=\frac{m}{x-1}$,
即$\left\{\begin{array}{l}{2-x=m}\\{x≠1}\end{array}\right.$,∴x=2-m(m≠1).
∴使关于x的分式方程$\frac{x}{x-1}$-2=$\frac{m}{x-1}$无解的m值是1.
故答案为:1.
点评 本题考查了分式方程的解法,考查了逆向思维方法,是基础题.

练习册系列答案
相关题目
5.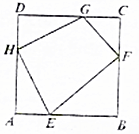 设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
 设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )| A. | 3 | B. | 6 | C. | $3\sqrt{2}$ | D. | $\frac{8}{3}$ |
7.已知F是抛物线x2=4y的焦点,直线y=kx-1与该抛物线交于第一象限内的零点A,B,若|AF|=3|FB|,则k的值是( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.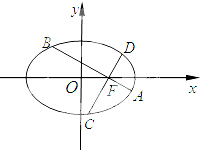 如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.
如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.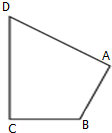 如图所示,在四边形ABCD中,|$\overrightarrow{CD}$|=4,|$\overrightarrow{AD}$|=5,$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,令|$\overrightarrow{BC}$|=x,|$\overrightarrow{BA}$|=y,则曲线y=f(x)可能是( )
如图所示,在四边形ABCD中,|$\overrightarrow{CD}$|=4,|$\overrightarrow{AD}$|=5,$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,令|$\overrightarrow{BC}$|=x,|$\overrightarrow{BA}$|=y,则曲线y=f(x)可能是( )

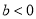 ,且
,且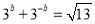 ,则
,则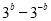 等于( )
等于( )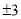 B.-2
B.-2