题目内容
19.t>0,关于x的方程|x|+$\sqrt{t-{x}^{2}}$=$\sqrt{2}$的解为集合A,则A中元素个数可能为0,2,3,4(写出所有可能).分析 化方程为$\sqrt{t-{x}^{2}}=\sqrt{2}-|x|$,得到两个函数所对应的图象,画出图象,数形结合得答案.
解答 解: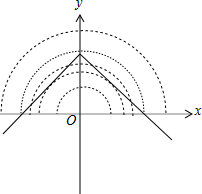 由|x|+$\sqrt{t-{x}^{2}}$=$\sqrt{2}$,得
由|x|+$\sqrt{t-{x}^{2}}$=$\sqrt{2}$,得
$\sqrt{t-{x}^{2}}=\sqrt{2}-|x|$,
由y=$\sqrt{t-{x}^{2}}$,得x2+y2=t(y≥0),
又$y=\sqrt{2}-|x|=\left\{\begin{array}{l}{-x+\sqrt{2},x≥0}\\{x+\sqrt{2},x<0}\end{array}\right.$,
作出图象如图:
由图可知,当0<t<1或t$>\sqrt{2}$时,A中元素个数为0;
当t=1时,A中元素个数为2;
当t=$\sqrt{2}$时,A中元素个数为3;
当1<t<$\sqrt{2}$时,A中元素个数为4.
故答案为:0,2,3,4.
点评 本题考查了根的存在性及根的个数判断,考查了数形结合与分类讨论的数学思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设实数x、y满足约束条件$\left\{\begin{array}{l}{3x-2y+4≥0}\\{x+y-4≤0}\\{x+ay-4≤0}\end{array}\right.$,已知z=2x+y的最大值是8,最小值是-5,则实数a的值为( )
| A. | 6 | B. | -6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
7.已知F是抛物线x2=4y的焦点,直线y=kx-1与该抛物线交于第一象限内的零点A,B,若|AF|=3|FB|,则k的值是( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
14.某校鲁班学习小组利用课余时间模拟制作奥运圣火采集器,已知他们制作采集器的抛物面的轴切线为经过定点P(1,2)的抛物线,则该抛物线的焦点与双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1在一三象限内的渐近线的距离为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$或$\frac{1}{16}$ | C. | $\frac{1}{16}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{1}{16}$ |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2. 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 的极坐标为
的极坐标为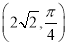 ,曲线
,曲线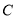 的参数方程为
的参数方程为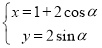 (
(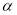 为参数).
为参数). 过
过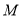 且与曲线
且与曲线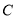 相切,求直线
相切,求直线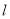 的极坐标方程;
的极坐标方程;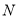 与点
与点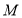 关于
关于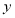 轴对称,求曲线
轴对称,求曲线 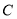 上的点到点
上的点到点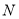 的距离的取值范围.
的距离的取值范围.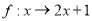 是集合
是集合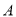 到集合
到集合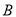 的映射,若
的映射,若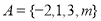 ,
,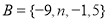 ,则
,则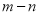 等于( )
等于( )