题目内容
已知正项数列{an},其前n项和Sn满足6Sn= +3an+2,且a1,a2,a6是等比数列{bn}的前三项.
+3an+2,且a1,a2,a6是等比数列{bn}的前三项.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=a1bn+a2bn-1+…+anb1,n∈N*,证明:3Tn+1=2bn+1-an+1(n∈N*).
 +3an+2,且a1,a2,a6是等比数列{bn}的前三项.
+3an+2,且a1,a2,a6是等比数列{bn}的前三项.(1)求数列{an}与{bn}的通项公式;
(2)记Tn=a1bn+a2bn-1+…+anb1,n∈N*,证明:3Tn+1=2bn+1-an+1(n∈N*).
(1)an=3n-2,bn=4n-1(2)见解析
(1)∵6Sn= +3an+2,①
+3an+2,①
∴6a1=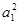 +3a1+2,解得a1=1或a1=2.
+3a1+2,解得a1=1或a1=2.
又6Sn-1=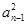 +3an-1+2(n≥2), ②
+3an-1+2(n≥2), ②
由①-②,得6an=( -
-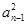 )+3(an-an-1),即(an+an-1)(an-an-1-3)=0.
)+3(an-an-1),即(an+an-1)(an-an-1-3)=0.
∵an+an-1>0,∴an-an-1=3(n≥2).
当a1=2时,a2=5,a6=17,此时a1,a2,a6不成等比数列,∴a1≠2;
当a1=1时,a2=4,a6=16,此时a1,a2,a6成等比数列,∴a1=1.
∴{an}是以1为首项3为公差的等差数列,{bn}是以1为首项4为公比的等比数列.
∴an=3n-2,bn=4n-1.
(2)由(1)得
Tn=1×4n-1+4×4n-2+…+(3n-5)×41+(3n-2)×40, ③
∴4Tn=1×4n+4×4n-1+7×4n-2+…+(3n-2)×41. ④
由④-③,得
3Tn=4n+3×(4n-1+4n-2+…+41)-(3n-2)=4n+12× -(3n-2)
-(3n-2)
=2×4n-(3n+1)-1=2bn+1-an+1-1,
∴3Tn+1=2bn+1-an+1(n∈N*).
 +3an+2,①
+3an+2,①∴6a1=
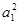 +3a1+2,解得a1=1或a1=2.
+3a1+2,解得a1=1或a1=2.又6Sn-1=
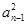 +3an-1+2(n≥2), ②
+3an-1+2(n≥2), ②由①-②,得6an=(
 -
-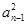 )+3(an-an-1),即(an+an-1)(an-an-1-3)=0.
)+3(an-an-1),即(an+an-1)(an-an-1-3)=0.∵an+an-1>0,∴an-an-1=3(n≥2).
当a1=2时,a2=5,a6=17,此时a1,a2,a6不成等比数列,∴a1≠2;
当a1=1时,a2=4,a6=16,此时a1,a2,a6成等比数列,∴a1=1.
∴{an}是以1为首项3为公差的等差数列,{bn}是以1为首项4为公比的等比数列.
∴an=3n-2,bn=4n-1.
(2)由(1)得
Tn=1×4n-1+4×4n-2+…+(3n-5)×41+(3n-2)×40, ③
∴4Tn=1×4n+4×4n-1+7×4n-2+…+(3n-2)×41. ④
由④-③,得
3Tn=4n+3×(4n-1+4n-2+…+41)-(3n-2)=4n+12×
 -(3n-2)
-(3n-2)=2×4n-(3n+1)-1=2bn+1-an+1-1,
∴3Tn+1=2bn+1-an+1(n∈N*).

练习册系列答案
相关题目
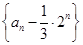 是等比数列;
是等比数列;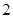 的等比数列
的等比数列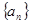 的各项都是正数,且
的各项都是正数,且 ,则
,则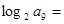 ( )
( )


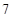
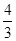 ,则{an}的前10项和等于( )
,则{an}的前10项和等于( )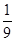 (1-310)
(1-310)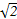 )
)