题目内容
4．
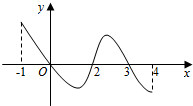已知函数f（x）的定义域为[-1，4]，部分对应值如表，| x | -1 | 0 | 2 | 3 | 4 |
| f（x） | 1 | 2 | 0 | 2 | 0 |
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据导函数图象，画出原函数的草图，利用1＜a＜2，即可得到函数y=f（x）-a的零点的个数．
解答 解：根据导函数图象，可得2为函数的极小值点，函数y=f（x）的图象如图所示：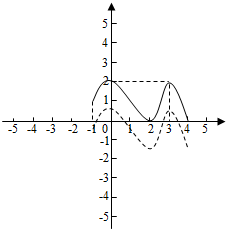
因为f（0）=f（3）=2，1＜a＜2，
所以函数y=f（x）-a的零点的个数为4个．
故选：D．
点评 本题主要考查导函数和原函数的单调性之间的关系．二者之间的关系是：导函数为正，原函数递增；导函数为负，原函数递减，本题属于中档题．
练习册系列答案
相关题目
17．
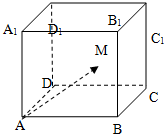如图，在棱长为2的正方体ABCD-A1B1C1D1内（含正方体表面）任取一点M，则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是（ ）
如图，在棱长为2的正方体ABCD-A1B1C1D1内（含正方体表面）任取一点M，则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是（ ）| A． | $\frac{5}{6}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
16．
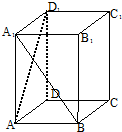如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，AA1=2AB，则异面直线A1B与AD1所成角的余弦值为（ ）
如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，AA1=2AB，则异面直线A1B与AD1所成角的余弦值为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
13．以直角坐标系的原点为极点x轴的正半轴为极轴，并在两种坐标系中取相同的长度单位．则曲线C1：ρ2-2ρcosθ-1=0上的点到曲线C2：$\left\{\begin{array}{l}{x=3-t}\\{y=1+t}\end{array}\right.$（t为参数）上的点的最短距离为（ ）
| A． | $2\sqrt{2}$ | B． | $\frac{{3\sqrt{2}}}{2}$ | C． | $\sqrt{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |