题目内容
在三棱锥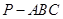 中,
中,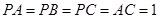 ,
,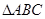 是等腰直角三角形,
是等腰直角三角形,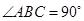 ,
,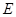 为
为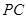 中点. 则
中点. 则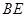 与平面
与平面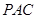 所成的角等于( )
所成的角等于( )
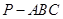 中,
中,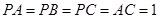 ,
,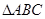 是等腰直角三角形,
是等腰直角三角形,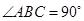 ,
,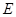 为
为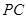 中点. 则
中点. 则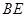 与平面
与平面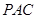 所成的角等于( )
所成的角等于( )A.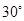 | B.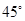 | C.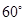 | D.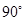 |
B
试题分析:先作PO⊥平面ABC,垂足为O,根据条件可证得点O为三角形ABC的外心,从而确定点O为AC的中点,然后证明BO是面PAC的垂线,从而得到∠BEO为BE与平面PAC所成的角,在直角三角形BOE中求解即可。
解: 如图:
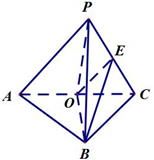
作PO⊥平面ABC,垂足为O,则∠POA=∠POB=∠POC=90°,,而PA=PB=PC,PO是△POA、△POB、△POC的公共边,∴△POA≌△POB≌△POC,∴AO=BO=CO,则点O为三角形ABC的外心,∵△ABC是等腰直角三角形,∠ABC=90°,∴点O为AC的中点,则BO⊥AC,而PO⊥BO,PO∩AC=O,∴BO⊥平面PAC,连接OE,∴∠BEO为BE与平面PAC所成的角,∵点O为AC的中点,E为PC中点,PA=PB=PC=AC=1,ABC是等腰直角三角形,∠ABC=90°,∴OE为中位线,且OE=
 ,BO=
,BO= 又∵∠BOE=90°,∴∠BEO=45°即BE与平面PAC所成的角的大小为45°,故选B.
又∵∠BOE=90°,∴∠BEO=45°即BE与平面PAC所成的角的大小为45°,故选B.点评:本题主要考查了三角形的外心的概念,以及直线与平面所成角和三角形全等等有关知识,同时考查了推理能力,属于中档题.

练习册系列答案
相关题目
 中,
中, ,
, ,点
,点 为线段
为线段 上的一点.现将
上的一点.现将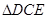 沿线段
沿线段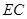 翻折到
翻折到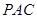 (点
(点 与点
与点 重合),使得平面
重合),使得平面 平面
平面 ,连接
,连接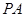 ,
, .
.
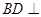 平面
平面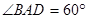 ,且点
,且点 的大小.
的大小.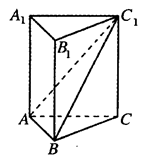
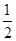
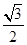
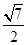
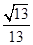
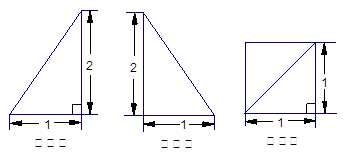
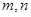 为两条不同的直线,
为两条不同的直线,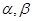 是两个不同的平面,下列命题正确的是
是两个不同的平面,下列命题正确的是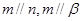 ,则
,则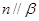
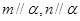 ,则
,则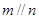
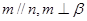 ,则
,则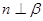
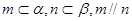 ,则
,则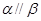
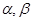 和直线
和直线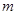 ,给出下列条件:①
,给出下列条件:①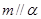 ;②
;②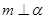 ;③
;③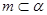 ;④
;④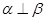 ;⑤
;⑤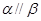 .则使
.则使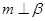 成立的充分条件是 .(填序号)
成立的充分条件是 .(填序号)
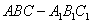 中,D是BC的中点,
中,D是BC的中点,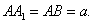
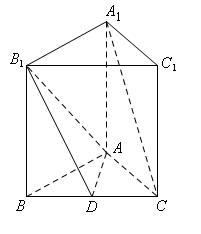
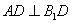 ;(Ⅱ)求证:
;(Ⅱ)求证: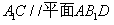 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥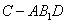 的体积.
的体积.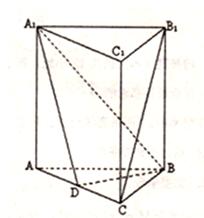
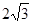 , BC=6.
, BC=6.