题目内容
(本小题满分12分)
如图:在底面为直角梯形的四棱锥P-ABCD中,AD‖BC ,∠ABC=90°,PA⊥平面ABCD, PA="3," AD="2," AB=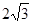 , BC=6.
, BC=6.

(1)求证:BD⊥平面PAC
(2)求二面角B-PC-A的大小.
如图:在底面为直角梯形的四棱锥P-ABCD中,AD‖BC ,∠ABC=90°,PA⊥平面ABCD, PA="3," AD="2," AB=
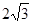 , BC=6.
, BC=6.
(1)求证:BD⊥平面PAC
(2)求二面角B-PC-A的大小.
(1)要证明线面垂直,可以结合向量法或者几何性质来证明,主要是对于线面判定的熟练的运用。
(2)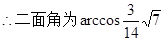
(2)
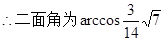
试题分析:解:(1)以
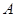 为原点,射线
为原点,射线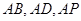 分别为
分别为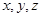 轴正向建立空间直角坐标系,则
轴正向建立空间直角坐标系,则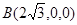 ,
,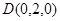 ,
,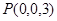 ,
,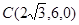
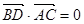 ,
,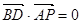
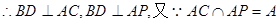
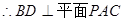 ----------------------------------(6分)
----------------------------------(6分)(2)平面
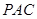 的法向量为
的法向量为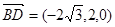
平面
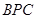 的法向量为
的法向量为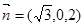
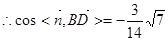
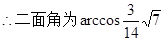 -----------------------------(12分)
-----------------------------(12分)点评:解决该试题的关键是能利用线面垂直的判定定理以及二面角的定义法或者是向量法来求解角的大小,属于基础题。

练习册系列答案
相关题目
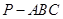 中,
中,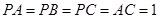 ,
,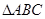 是等腰直角三角形,
是等腰直角三角形,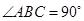 ,
,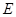 为
为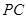 中点. 则
中点. 则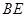 与平面
与平面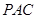 所成的角等于( )
所成的角等于( )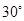
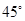
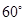
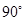
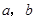 为两条直线,
为两条直线,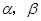 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( ) 所成的角相等,则
所成的角相等,则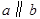
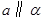 ,
,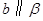 ,
,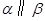 ,则
,则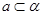 ,
,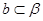 ,
,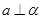 ,
,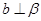 ,
, ,则
,则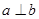
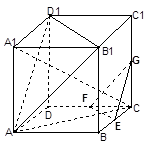
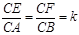 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 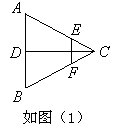
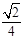 ,求k的值.
,求k的值. 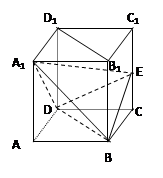
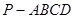 中,平面
中,平面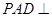 平面
平面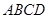 ,
,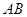 ∥
∥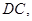
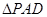 是正三角形,已知
是正三角形,已知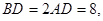
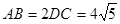
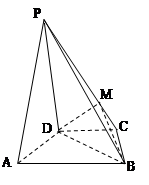
 是
是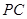 上的一点,求证:平面
上的一点,求证:平面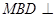 平面
平面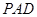 ;
;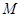 、
、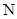 分别是
分别是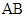 、
、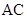 的中点,
的中点,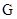 是
是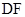 上的一动点,主视图与俯视图都为正方形。
上的一动点,主视图与俯视图都为正方形。

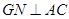 ;
;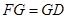 时,在棱
时,在棱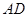 上确定一点
上确定一点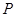 ,使得
,使得 ∥平面
∥平面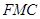 ,并给出证明。
,并给出证明。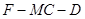 的平面角余弦值。
的平面角余弦值。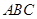 一边BC在平面
一边BC在平面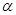 内,顶点A在平面
内,顶点A在平面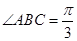 ,三角形所在平面与
,三角形所在平面与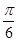 ,则直线
,则直线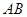 与
与