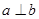题目内容
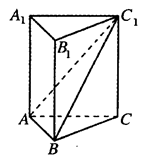
如图,在正三棱柱ABC-A1B1C1中,AB=2.若二面角C-AB-C1的大小为60°,则异面直线A1B1和BC1所成角的余弦值为

A.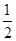 | B.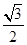 | C.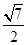 | D.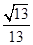 |
D
试题分析:如图所示,
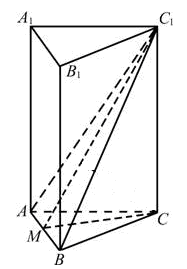
取AB中点M,由C1A=C1B知C1M⊥AB,CM⊥AB,则∠C1MC为二面角C-AB-C1的平面角,在Rt△C1CM中,cos60°=
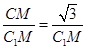 ,∴C1M=2
,∴C1M=2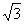 ,∵AB∥
,∵AB∥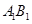 ,∴∠C1BM为所求的异面直线夹角,Rt△C1MB中,tan∠C1BM=
,∴∠C1BM为所求的异面直线夹角,Rt△C1MB中,tan∠C1BM=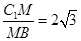 ,∴cos∠C1BM=
,∴cos∠C1BM=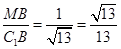 即异面直线A1B1和BC1所成角的余弦值为
即异面直线A1B1和BC1所成角的余弦值为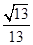 ,故选D
,故选D点评:利用异面直线夹角的概念是解决此类问题的常用方法,属基础题

练习册系列答案
相关题目
 个
个 个
个 个
个 △ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=
△ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=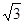 ,则点P 到△ABC的斜边AB的距离是( )
,则点P 到△ABC的斜边AB的距离是( ) 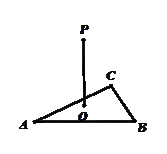
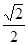
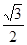
 与等腰直角三角形
与等腰直角三角形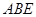 所在的平面互相垂直.
所在的平面互相垂直.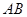 ∥
∥ ,
, ,
,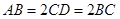 ,
,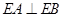 .
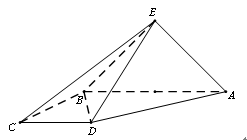
.
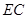 与平面
与平面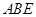 所成角的正弦值;
所成角的正弦值;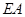 上是否存在点
上是否存在点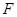 ,使
,使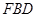 ?若存在,求出
?若存在,求出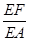 ;若不存在,说明理由.1
;若不存在,说明理由.1 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.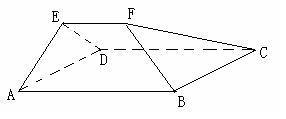
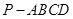 的底面为等腰梯形,
的底面为等腰梯形,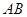 ∥
∥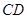 ,
,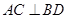 ,垂足为
,垂足为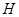 ,
,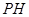 是四棱锥的高。
是四棱锥的高。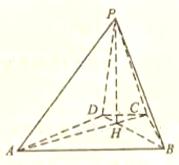
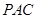
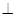 平面
平面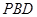 ;
;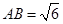 ,
,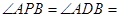 60°,求四棱锥
60°,求四棱锥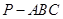 中,
中,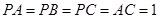 ,
,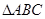 是等腰直角三角形,
是等腰直角三角形,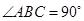 ,
,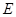 为
为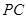 中点. 则
中点. 则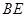 与平面
与平面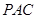 所成的角等于( )
所成的角等于( )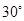
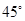
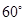
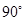
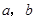 为两条直线,
为两条直线,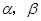 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( ) 所成的角相等,则
所成的角相等,则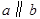
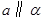 ,
,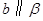 ,
,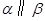 ,则
,则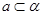 ,
,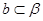 ,
,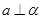 ,
,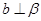 ,
, ,则
,则