题目内容
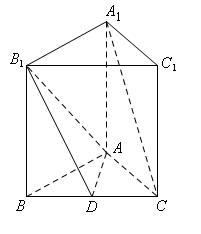
(本小题满分13分)如图,正三棱柱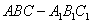 中,D是BC的中点,
中,D是BC的中点,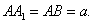
(Ⅰ)求证: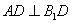 ;(Ⅱ)求证:
;(Ⅱ)求证: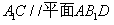 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥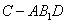 的体积.
的体积.
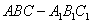 中,D是BC的中点,
中,D是BC的中点,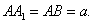

(Ⅰ)求证:
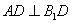 ;(Ⅱ)求证:
;(Ⅱ)求证: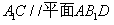 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥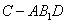 的体积.
的体积.(1)根据三棱柱中BB1⊥平面ABC,结合AD⊥BD,根据三垂线定理得,AD⊥B1D,得到证明。
(2)要证明线面平行,关键是对于DE∥A1C.的证明。
(3)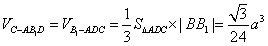
(2)要证明线面平行,关键是对于DE∥A1C.的证明。
(3)
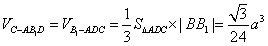
试题分析:(Ⅰ)证明:∵ABC—A1B1C1是正三棱柱,∴BB1⊥平面ABC,∴BD是B1D在平面ABC上的射影在正△ABC中,∵D是BC的中点,∴AD⊥BD,根据三垂线定理得,AD⊥B1D
(Ⅱ)解:连接A1B,设A1B∩AB1 = E,连接DE.∵AA1=AB ∴四边形A1ABB1是正方形,∴E是A1B的中点,又D是BC的中点,∴DE∥A1C. ………………………… 7分∵DE
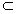 平面AB1D,A1C
平面AB1D,A1C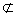 平面AB1D,∴A1C∥平面AB1D. ……………………9分
平面AB1D,∴A1C∥平面AB1D. ……………………9分 (Ⅲ)
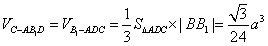 ……13分
……13分点评:解决该试题的关键是能利用线面平行的判定定理,以及面面垂直的性质定理来证明线线垂直,同时结合体积公式计算,属于基础题。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 △ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=
△ABC两直角边分别为3、4,PO⊥面ABC,O是△ABC的内心,PO=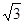 ,则点P 到△ABC的斜边AB的距离是( )
,则点P 到△ABC的斜边AB的距离是( ) 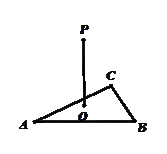
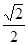
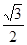
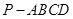 的底面为等腰梯形,
的底面为等腰梯形,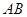 ∥
∥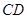 ,
,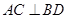 ,垂足为
,垂足为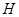 ,
,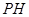 是四棱锥的高。
是四棱锥的高。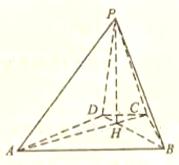
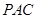
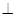 平面
平面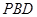 ;
;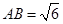 ,
,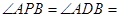 60°,求四棱锥
60°,求四棱锥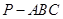 中,
中,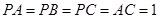 ,
,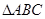 是等腰直角三角形,
是等腰直角三角形,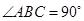 ,
,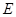 为
为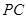 中点. 则
中点. 则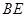 与平面
与平面 所成的角等于( )
所成的角等于( )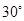
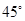
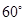
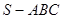 中,
中,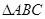 是边长为4的正三角形,
是边长为4的正三角形,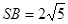 ,
,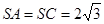 ,
,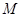 、
、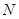 分别是
分别是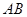 、
、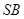 的中点;
的中点;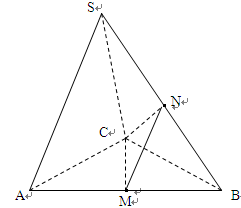
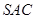
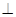 平面
平面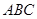 ;
;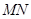 与平面
与平面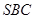 所成角的正弦值。
所成角的正弦值。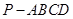 中,平面
中,平面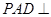 平面
平面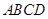 ,
,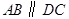 ,
,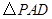 是等边三角形,已知
是等边三角形,已知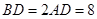 ,
,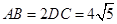 .
.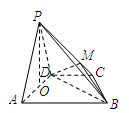
 是
是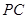 上的一点,证明:平面
上的一点,证明:平面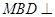 平面
平面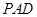 ;
;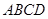 中,
中,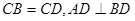 ,且E、F分别是AB、BD的中点,
,且E、F分别是AB、BD的中点,
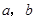 为两条直线,
为两条直线,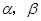 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( ) 所成的角相等,则
所成的角相等,则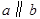
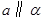 ,
,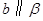 ,
,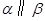 ,则
,则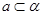 ,
,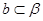 ,
,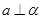 ,
,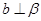 ,
, ,则
,则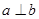
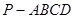 中,平面
中,平面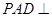 平面
平面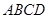 ,
,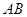 ∥
∥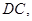
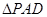 是正三角形,已知
是正三角形,已知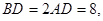
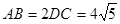
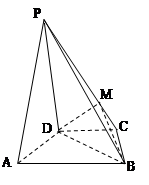
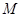 是
是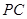 上的一点,求证:平面
上的一点,求证:平面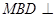 平面
平面 ;
;