题目内容
12.已知函数f(x)=2sin(2x-$\frac{π}{3}$)+1.(1)求f(x)的最大值及相应的x的值;
(2)若不等式f2(x)-2m•f(x)+m2-4<0在x∈[$\frac{π}{4}$,$\frac{π}{2}$]上恒成立,求实数m的取值范围.
分析 (1)由条件利用正弦函数的最大值求得函数f(x)取得最大值.
(2)由题意可得m-2<f(x)<2+m恒成立,再根据x∈[$\frac{π}{4}$,$\frac{π}{2}$],求得 f(x)=2sin(2x-$\frac{π}{3}$)+1∈[1,3],可得$\left\{\begin{array}{l}{m-2<1}\\{m+2>3}\end{array}\right.$,由此求得m的范围.
解答 解:(1)对于函数f(x)=2sin(2x-$\frac{π}{3}$)+1,当2x-$\frac{π}{3}$=2kπ+$\frac{π}{2}$,k∈Z时,
即x=kπ+$\frac{5π}{12}$时,函数f(x)取得最大值为2+1=3.
(2)不等式f2(x)-2m•f(x)+m2-4<0在x∈[$\frac{π}{4}$,$\frac{π}{2}$]上恒成立,
即[f(x)-m]2<4,即-2<f(x)-m<2,即 m-2<f(x)<2+m恒成立.
再根据x∈[$\frac{π}{4}$,$\frac{π}{2}$],可得2x-$\frac{π}{3}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],∴sin(2x-$\frac{π}{3}$)∈[$\frac{1}{2}$,1],
∴f(x)=2sin(2x-$\frac{π}{3}$)+1∈[1,3].
∴$\left\{\begin{array}{l}{m-2<1}\\{m+2>3}\end{array}\right.$,求得1<m<3.
点评 本题主要考查正弦函数的最大值,函数的恒成立问题,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知a+$\frac{1}{a}$=3,则a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$等于( )
| A. | 2 | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | $±\sqrt{5}$ |
1.定义在R上的函数y=f(x)的值域为[0,1],则y=f(x+1)的值域为( )
| A. | [0,1] | B. | [1,2] | C. | [-1,0] | D. | 无法确定 |
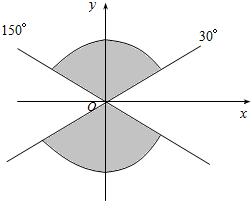 已知角α的终边在图中阴影部分所表示的范围内(不包括边界),则α的取值范围为{α|k•180°+30°<α<k•180°+150°,k∈Z}.
已知角α的终边在图中阴影部分所表示的范围内(不包括边界),则α的取值范围为{α|k•180°+30°<α<k•180°+150°,k∈Z}.