题目内容
2.设数列{an} 满足a1=a,an+1=can+1-c,c∈N*,其中a、c为实数,且c≠0,则数列{an} 的通项公式为an=1+(a-1)cn-1.分析 通过对an+1=can+1-c变形可知an+1-1=c(an-1),进而可知数列{an-1} 是以a-1为首项、c为公比的等比数列,计算即得结论.
解答 解:∵an+1=can+1-c,c∈N*,
∴an+1-1=c(an-1),c∈N*,
又∵a1-1=a-1,
∴数列{an-1} 是以a-1为首项、c为公比的等比数列,
∴an-1=(a-1)cn-1,
∴an=1+(a-1)cn-1,
故答案为:1+(a-1)cn-1.
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
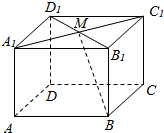 如图所示,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,设M是上底面A1B1C1D1的中心.
如图所示,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,设M是上底面A1B1C1D1的中心.