题目内容
为了在夏季降温和冬季供暖时减少能源损耗,房屋的房顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用为C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0
(0 x
x 10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
(1)f(x)="20C(x)+" C1(x)=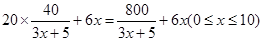
(2)当隔热层修建5cm厚时,总费用达到最小值70万元。
解析试题分析:(1)设隔热层厚度为xcm,由题设,每年能源消耗费用为C(x)=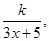
再由C(0)=8,得k=40,因此C(x)=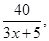 而建造费用为C1(x)=6x.
而建造费用为C1(x)=6x.
最后得隔热层建造费用与20年的能源消耗费用之和为
f(x)="20C(x)+" C1(x)=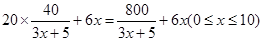
(2)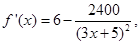 令
令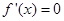 即
即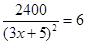
解得x=5,x=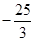 (舍去)
(舍去)
当0<x<5时,f’(x)<0,当5<x<10时f’(x)>0,故x=5是f(x)的最小值点,对应的最小值为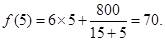
当隔热层修建5cm厚时,总费用达到最小值70万元。
考点:函数模型,应用导数研究函数的最值。
点评:中档题,作为函数应用问题,首先应注意“审清题意,设出变量,列出函数关系,确定函数最值”。在研究函数最值时,往往利用均值定理或导数。应用均值定理时,要注意“已知,二定,三相等”,缺一不可。本题利用导数,在指定自变量范围内,只有一个极值点,因此,可以断定其即为最值点。

2013年,首都北京经历了59年来雾霾天气最多的一个月。经气象局统计,北京市从1月1日至1月30日这30天里有26天出现雾霾天气。《环境空气质量指数(AQI)技术规定(试行)》将空气质量指数分为六级:其中,中度污染(四级),指数为151—200;重度污染(五级),指数为201—300;严重污染(六级),指数大于300. 下面表1是该观测点记录的4天里,AQI指数 与当天的空气水平可见度
与当天的空气水平可见度 (千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果,
(千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果,
表1:AQI指数 与当天的空气水平可见度
与当天的空气水平可见度 (千米)情况
(千米)情况
AQI指数 |  |  |  |  |
空气可见度 (千米) (千米) |  |  |  |  |
| AQI指数 |  |  |  |  |  |
| 频数 | 3 | 6 | 12 | 6 | 3 |
 ,根据表1的数据,求出
,根据表1的数据,求出 关于
关于 的线性回归方程;
的线性回归方程;(Ⅱ)根据表2估计这30天AQI指数的平均值.
(用最小二乘法求线性回归方程系数公式
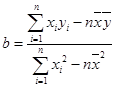 ,
, )
)  ,且不等式
,且不等式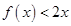 的解集为
的解集为 .
. 有两个相等的实根,求
有两个相等的实根,求 的解析式;
的解析式; ,求实数
,求实数 的取值范围;
的取值范围; 存在零点,并求出零点.
存在零点,并求出零点.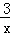 )元.
)元. )元;
)元;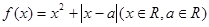 .
. 时,求
时,求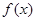 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的二次项系数为
的二次项系数为 ,满足不等式
,满足不等式 的解集为(1,3),且方程
的解集为(1,3),且方程 有两个相等的实根,求
有两个相等的实根,求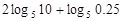 ;
;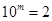 ,
,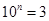 ,求
,求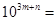
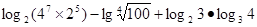 。
。 是奇函数,
是奇函数, 是偶函数。
是偶函数。 的值;
的值; 若
若 对任意
对任意 恒成立,求实数
恒成立,求实数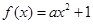 (
( ),
), .
. 与
与 处具有公共切线,求
处具有公共切线,求 的值;
的值; 时,求函数
时,求函数 在区间
在区间 上的最大值.
上的最大值.