题目内容
19.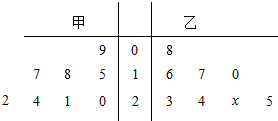 如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.
如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.(Ⅰ)若甲、乙两运动员得分的中位数相同,求数字x的值;
(Ⅱ)若x取0,1,2,…,9,十个数字是等可能的,求甲的平均得分不超过乙的平均得分的概率.
分析 (I)由茎叶图可先求甲、乙的中位数,进而可求x
(II)结合茎叶图先求甲,乙的平均分,结合已知条件可求x的取值,进而可求
解答 解:(I)由茎叶图可知,甲的中位数为$\frac{18+20}{2}=19$(1分)
乙的中位数为$\frac{17+20+x}{2}=\frac{37+x}{2}$
则$\frac{37+x}{2}=19$,x=1
II)由茎叶图可知,甲的平均分为$\frac{1}{8}×(9+15+17+18+20+21+22+24)=18.25$(5分)
乙的平均分为$\frac{1}{8}×(8+10+16+17+23+24+25+20+x)$=$\frac{143+x}{8}$(6分)
由题意可得,18.25$≤\frac{143+x}{8}$(8分)
解可得,x≥3(9分)
∴x可取3,4,5,6,7,8,9(10分)
甲的平均得分不超过乙的平均得分的概率为$\frac{7}{10}$(12分)
点评 本题主要考查了一组数据平均数、中位数的求解,解题的关键是茎叶图的识别.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
7.直线l:y=kx-1与圆x2+y2=1相交于A、B两点,则△OAB的面积最大值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
4.已知a=0.80.2,b=0.80.5,c=5.20.1,则这三个数的大小关系为( )
| A. | b<a<c | B. | a<b<c | C. | c<a<b | D. | c<b<a |
11.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的表面积是( )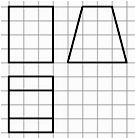

| A. | 42+6$\sqrt{17}$ | B. | 30+6$\sqrt{17}$ | C. | 66 | D. | 44 |
8.在△ABC中,若C=90°,三边为a,b,c,则$\frac{a+b}{c}$的范围是( )
| A. | ($\sqrt{2}$,2) | B. | (1,$\sqrt{2}$] | C. | (0,$\sqrt{2}$] | D. | [$\frac{{\sqrt{2}}}{2}$,$\sqrt{2}$] |
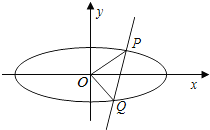 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).