题目内容
10.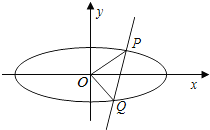 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).(Ⅰ)求椭圆C的方程;
(Ⅱ)已知直线l与椭圆C相交于P,Q两点,以PQ为直径的圆恒过原点O,试问原点O到直线l的距离d是否为定值?若是,求出其定值,若不是,请说明理由.
分析 (Ⅰ)根据椭圆过点(0,1)即可知道b=1,从而由离心率可求得a=2,从而写出椭圆的标准方程;
(Ⅱ)设P(x1,y1),Q(x2,y2),根据条件知道OP⊥OQ,从而得到x1x2+y1y2=0,直线l分不存在斜率和存在斜率两种情况:不存在斜率时设l的方程为x=t,根据x1x2+y1y2=0即可求出t,从而求出原点O到直线l的距离d=$\frac{2\sqrt{5}}{5}$;存在斜率时,设l方程为y=kx+m,带入椭圆方程,由韦达定理即可求出x1x2,x1+x2,带入x1x2+y1y2=0便可得到${k}^{2}+1=\frac{5}{4}{m}^{2}$,由点到直线的距离即可求出d=$\frac{2\sqrt{5}}{5}$,从而综合以上两种情况即可得到原点O到直线l的距离d是定值,且可写出定值d.
解答 解:(Ⅰ)由已知,b=1,$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}=\frac{\sqrt{3}}{2}$;
∴a2=4;
∴椭圆C的标准方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)∵以PQ为直径的圆恒过原点O;
∴OP⊥OQ;
∴$\overrightarrow{OP}•\overrightarrow{OQ}=0$;
设P(x1,y1),Q(x2,y2),则x1x2+y1y2=0;
(1)当直线l的斜率不存在时,设直线l的方程为x=t,则:
x1=x2=t,${y}_{1}{y}_{2}=\frac{{t}^{2}}{4}-1$,代入x1x2+y1y2=0得,${t}^{2}+\frac{{t}^{2}}{4}-1=0$;
∴$t=±\frac{2\sqrt{5}}{5}$;
∴O到直线l的距离d=$\frac{2\sqrt{5}}{5}$;
(2)当直线l的斜率存在时,设直线l的方程为y=kx+m;
∵x1x2+y1y2=0;
∴x1x2+(kx1+m)(kx2+m)=0;
∴$(1+{k}^{2}){x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}=0$①;
将y=kx+m代入$\frac{{x}^{2}}{4}+{y}^{2}=1$得,(1+4k2)x2+8kmx+4(m2-1)=0;
∴△=4k2-m2+1>0;
${x}_{1}+{x}_{2}=\frac{-8km}{1+4{k}^{2}},{x}_{1}{x}_{2}=\frac{4({m}^{2}-1)}{1+4{k}^{2}}$;
带入①得:5m2=4(k2+1);
∴d=$\frac{|m|}{\sqrt{1+{k}^{2}}}=\frac{|m|}{\frac{\sqrt{5}}{2}|m|}=\frac{2\sqrt{5}}{5}$;
综上得当直线l满足题意时,原点O到直线l的距离d为定值且d=$\frac{2\sqrt{5}}{5}$.
点评 考查椭圆的标准方程,椭圆离心率的概念及计算公式,椭圆标准方程中a,b,c的关系:a2=b2+c2,圆的直径对的圆周角为直角,两向量垂直时数量积为0,在用斜截式方程表示直线时需考虑直线存在斜率和不存在斜率两种情况,以及韦达定理,点到直线的距离公式.

 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | “a、b都是有理数”的否定是“a、b都不是有理数” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | “x=-1”是“x2-5x-6=0”的必要不充分条件 |
| A. | m≥1 | B. | m≥1且m≠1 | C. | m≥1且m≠5 | D. | 0<m<5且m≠1 |

| A. | $\frac{3π}{2}$ | B. | $\frac{7π}{4}$ | C. | 2π-1 | D. | 4π-1 |
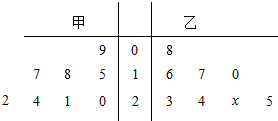 如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.
如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.