题目内容
9.已知函数f(x)=$\left\{{\begin{array}{l}{{{log}_2}(x+1),x>1}\\{x-1,x≤1}\end{array}}$,若关于x的方程f[f(x)]=a有解,则实数a的取值范围是(-∞,-1]∪(1,+∞).分析 等价于方程f(t)=a①有解且f(x)=t②也要有解,分别可得a的范围,综合可得.
解答 解:由题意知:当x>1时,f(x)=log2(x+1)∈(1,+∞),
当x≤1时,f(x)=x-1∈(-∞,0],
f(x)图象如下: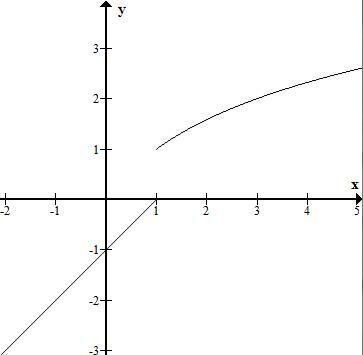
令f(x)=t,则方程f[f(x)]=a有解
等价于方程f(t)=a①有解且f(x)=t②也要有解,
由方程①有解可得a≤0或a>1,
由方程②有解则①的解t满足t≤0或t>1,
所以a≤-1或a>1,
综上可得a≤-1或a>1,
故答案为:(-∞,-1]∪(1,+∞)
点评 本题考查函数的零点,等价转化是解决问题的关键,属基础题.

练习册系列答案
相关题目
17.某舰艇在A处测得遇险渔船在北偏东45°距离为10海里的C处,此时得知,该渔船沿北偏东105°方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是( )小时.
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | 1 |
4.下列说法中一定正确的是( )
| A. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | B. | 若ac2>bc2,则a>b | C. | 若a>b,则ac>bc | D. | 若a>b,则(${\frac{1}{2}}$)a>(${\frac{1}{2}}$)b |
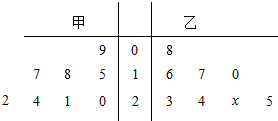 如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.
如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.