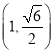Question

【题目】某生物探测器在水中逆流行进时，所消耗的能量为E＝cvnT，其中v为行进时相对于水的速度，T为行进时的时间（单位：h），c为常数，n为能量次级数，如果水的速度为4km/h，该生物探测器在水中逆流行进200km．

（1）求T关于v的函数关系式；

（2）①当能量次级数为2时，求探测器消耗的最少能量；

②当能量次级数为3时，试确定v的大小，使该探测器消耗的能量最少．

Answer 1

【答案】（1）T，（v＞4）；（2）①3200c②6

【解析】

（1）由题意得，化简即可得解；

（2）①由题意得，利用基本不等式即可得解；②由题意，求导得，确定单调性即可得解.

（1）由题意得，该探测器相对于河岸的速度为，

又该探测器相对于河岸的速度比相对于水的速度小4km/h，即为v﹣4，

则v﹣4，即T，（v＞4）；

（2）①当能量次级数为2时，由（1）知，v＞4，

≥200c[28]＝3200c，当且仅当v﹣4，即v＝8km/h时取等号，

②当能量次级数为3时，由（1）知，v＞4，

则，由，解得v＝6，

即当v＜6时，，当v＞6时，，

即当v＝6时，函数E取得最小值为E＝21600c．