题目内容
【题目】抛物线C:y2=2px(p>0)的焦点是F,直线y=2与抛物线C的交点到F的距离等于2.
(1)求抛物线C的方程;
(2)过点(2,0)斜率为k的直线l交抛物线C于A、B两点,O为坐标原点,直线AO与直线x=﹣2相交于点P,求证:BP∥x轴.
【答案】(1)y2=4x;(2)见解析
【解析】
(1)求出直线y=2与抛物线C的交点的横坐标,应用焦半径公式,即可求解;
(2)设出直线l的方程,与抛物线方程联立,建立A、B纵坐标关系,再利用![]() 三点共线,求出
三点共线,求出![]() 纵坐标关系,即可证明结论.
纵坐标关系,即可证明结论.
(1)由题意得直线与抛物线的交点坐标:(![]() ,2),
,2),
所以![]() 2 且p>0解得:p=2,
2 且p>0解得:p=2,
所以抛物线C的方程:y2=4x;
(2)由题意得:直线l的斜率不为零,
设直线l的方程:x=my+2,
代入抛物线方程得:y2﹣4my﹣8=0,
设A(x0,y0),B(x',y'),y0y'=﹣8,y'![]() ,
,
所以B(x',![]() ),直线OA的方程:y
),直线OA的方程:y![]() x
x![]() x,
x,
与x=﹣2的交点P(﹣2,![]() ),
),
![]() BP∥x轴.
BP∥x轴.

【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
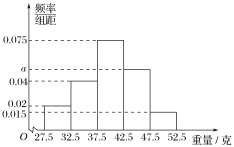
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?