题目内容
【题目】在平面直角坐标系![]() 中已知椭圆
中已知椭圆![]() 过点
过点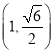 ,其左、右焦点分别为
,其左、右焦点分别为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆E的方程;
(2)若A,B分别为椭圆E的左、右顶点,动点M满足![]() ,且MA交椭圆E于点P.
,且MA交椭圆E于点P.
(i)求证:![]() 为定值;
为定值;
(ii)设PB与以PM为直径的圆的另一交点为Q,问:直线MQ是否过定点,并说明理由.
【答案】(1) ![]() (2) (i)证明见解析,定值为4 (ii)直线
(2) (i)证明见解析,定值为4 (ii)直线![]() 过定点
过定点![]() .
.
【解析】
(1)由题意得离心率公式和点满足的方程,结合椭圆的![]() 的关系,可得
的关系,可得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)(i)设![]()
![]() ,求得直线MA的方程,代入椭圆方程,解得点P的坐标,再由向量的数量积的坐标表示,计算即可得证;
,求得直线MA的方程,代入椭圆方程,解得点P的坐标,再由向量的数量积的坐标表示,计算即可得证;
(ii)直线MQ过定点O(0,0).先求得PB的斜率,再由圆的性质可得MQ⊥PB,求出MQ的斜率,再求直线MQ的方程,即可得到定点.
解:(1)易得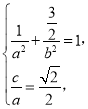 且
且![]() ,
,
解得
所以椭圆E的方程为![]()
(2)设![]()
![]() ,
,
①易得直线![]() 的方程为:
的方程为:![]() ,
,
代入椭圆![]() 得,
得,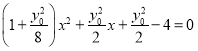 ,
,
由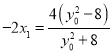 得,
得,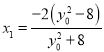 ,从而
,从而![]() ,
,
所以示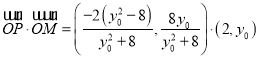
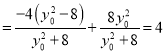 ,
,
②直线![]() 过定点
过定点![]() ,理由如下:
,理由如下:
依题意,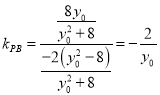 ,
,
由![]() 得,
得,![]() ,
,
则![]() 的方程为:
的方程为:![]() ,即
,即![]() ,
,
所以直线![]() 过定点
过定点![]() .
.

【题目】某人沿固定路线开车上班,沿途共有![]() 个红绿灯,他对过去
个红绿灯,他对过去![]() 个工作日上班途中的路况进行了统计,得到了如表的数据:
个工作日上班途中的路况进行了统计,得到了如表的数据:
上班路上遇见的红灯数 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
若一路绿灯,则他从家到达公司只需用时![]() 分钟,每遇一个红灯,则会多耗时
分钟,每遇一个红灯,则会多耗时![]() 分钟,以频率作为概率的估计值
分钟,以频率作为概率的估计值
(1)试估计他平均每天上班需要用时多少分钟?
(2)若想以不少于![]() 的概率在早上
的概率在早上![]() 点前(含
点前(含![]() 点)到达公司,他最晚何时要离家去公司?
点)到达公司,他最晚何时要离家去公司?
(3)公司规定,员工应早上![]() 点(含
点(含![]() 点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款
点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款![]() 元.因某些客观原因,在接下来的
元.因某些客观原因,在接下来的![]() 个工作日里,他每天早上只能
个工作日里,他每天早上只能![]() 从家出发去公司,求他因迟到而被罚款的期望.
从家出发去公司,求他因迟到而被罚款的期望.
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|
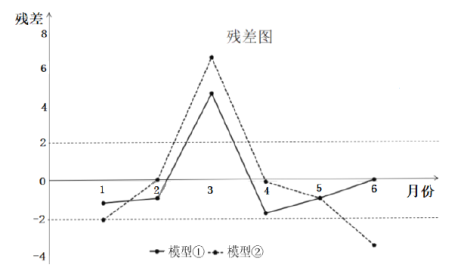
(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程;
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
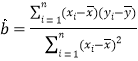
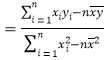 ,
,![]() .
.
【题目】某校为了了解高一新生是否愿意参加军训,随机调查了80名新生,得到如下2×2列联表
愿意 | 不愿意 | 合计 | |
男 | x | 5 | M |
女 | y | z | 40 |
合计 | N | 25 | 80 |
(1)写出表中x,y,z,M,N的值,并判断是否有99.9%的把握认为愿意参加军训与性别有关;
(2)在被调查的不愿意参加军训的学生中,随机抽出3人,记这3人中男生的人数为ξ,求ξ的分布列和数学期望.
参考公式: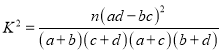
附:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |