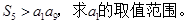题目内容
已知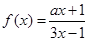 ,且方程
,且方程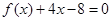 有两个不同的正根,其中一根是另一根的
有两个不同的正根,其中一根是另一根的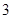 倍,记等差数列
倍,记等差数列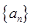 、
、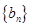 的前
的前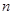 项和分别为
项和分别为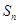 ,
,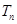 且
且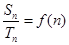 (
(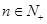 )。
)。
(1)若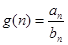 ,求
,求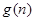 的最大值;
的最大值;
(2)若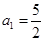 ,数列
,数列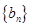 的公差为3,试问在数列
的公差为3,试问在数列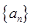 与
与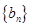 中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列
中是否存在相等的项,若存在,求出由这些相等项从小到大排列得到的数列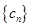 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
(3)若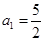 ,数列
,数列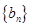 的公差为3,且
的公差为3,且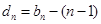 ,
,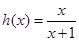 .
.
试证明: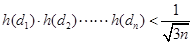 .
.
(1)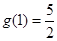 (2)在数列
(2)在数列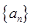 与
与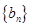 中不存在相等的项。
中不存在相等的项。
(3)运用数序归纳法来证明与自然数相关的命题得到结论。
解析试题分析:解:(1)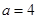 ,
,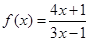 ,
,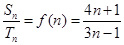
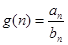
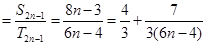 故
故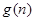 的最大值为
的最大值为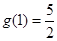 。
。
(2)由(1)知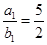 ,
,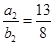 可得
可得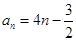 ,
,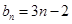
令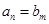 ,
,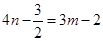 可得:
可得: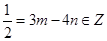 矛盾
矛盾
所以在数列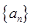 与
与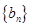 中不存在相等的项。
中不存在相等的项。
(3)证明:∵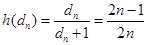 ∴要证
∴要证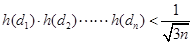
即要证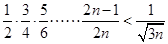 (直接用数学归纳法证明不出)
(直接用数学归纳法证明不出)
只要证明 (再用数学归纳法证明即可)
(再用数学归纳法证明即可)
提示:当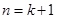 时,只要证:
时,只要证: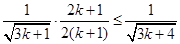
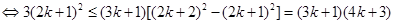
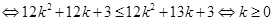
考点:数列的性质以及不等式的证明
点评:主要是考查了数列与不等式以及数列的性质的运用,属于难度题。

练习册系列答案
相关题目
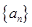 和等比数列
和等比数列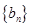 中,a1=2, 2b1=2, b6=32,
中,a1=2, 2b1=2, b6=32, 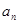 和
和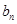 ;
;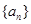 中,
中,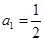 ,点
,点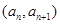 在直线
在直线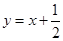 上.
上.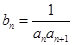 ,求数列
,求数列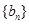 的前n项和
的前n项和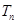 .
.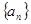 是一个等差 数列,且
是一个等差 数列,且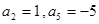 。
。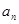 ; (2)求
; (2)求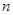 项和
项和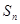 的最大值。
的最大值。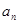 }的前
}的前 项和为
项和为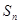 ,已知
,已知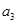 =
= ,
,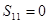 .
.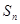 ;
;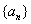 中,
中, 为前n项和,且满足
为前n项和,且满足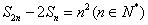
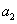 及数列
及数列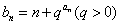 ,求数列
,求数列 的前n项和
的前n项和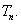
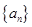 的前四项和为10,且
的前四项和为10,且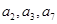 成等比数列
成等比数列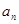
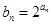 ,求数列
,求数列 的前
的前 项和
项和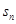
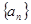 中,
中,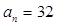 ,
, ,
, 为公差为11的等差数列,求
为公差为11的等差数列,求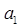 ;
;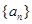 是以
是以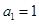 为首项、公比为
为首项、公比为 的等比数列,求
的等比数列,求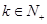 总有:
总有: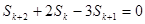
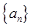 的公差
的公差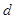 =1,前
=1,前 项和为
项和为 .
.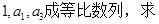
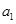 ;
;