题目内容
设等差数列{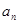 }的前
}的前 项和为
项和为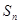 ,已知
,已知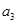 =
= ,
,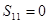 .
.
(Ⅰ) 求数列{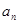 }的通项公式;
}的通项公式;
(Ⅱ)求数列{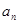 }的前n项和
}的前n项和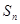 ;
;
(Ⅲ)当n为何值时,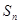 最大,并求
最大,并求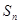 的最大值.
的最大值.
(Ⅰ)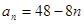 (Ⅱ)
(Ⅱ)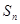 =
=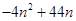 (Ⅲ)当
(Ⅲ)当 或
或 时,
时,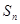 最大,且
最大,且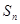 的最大值为120.
的最大值为120.
解析试题分析:(Ⅰ)依题意有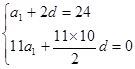 ,解之得
,解之得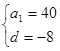 ,∴
,∴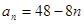 .
.
(Ⅱ)由(Ⅰ)知,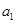 =40,
=40,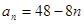 ,
,
∴ 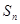 =
=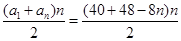 =
=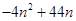 .
.
(Ⅲ)由(Ⅱ)有,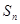 =
=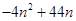 =-4
=-4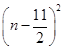 +121,
+121,
故当 或
或 时,
时,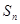 最大,且
最大,且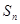 的最大值为120.
的最大值为120.
考点:本小题主要考查等差数列中基本量的求解和二次函数求最值在数列中的应用.
点评:等差数列是一类比较重要的数列,它的基本量之间的关系经常考查,要牢固掌握它们之间的关系,灵活求解.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
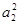 ,且S1,S2,S4成等比数列,
,且S1,S2,S4成等比数列,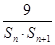 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.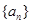 中,
中,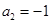 且
且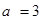 求等差数列
求等差数列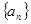 是等差数列,且
是等差数列,且
 求数列
求数列 前n项和的公式.
前n项和的公式.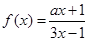 ,且方程
,且方程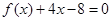 有两个不同的正根,其中一根是另一根的
有两个不同的正根,其中一根是另一根的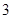 倍,记等差数列
倍,记等差数列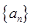 、
、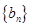 的前
的前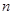 项和分别为
项和分别为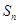 ,
,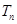 且
且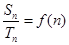 (
(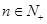 )。
)。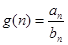 ,求
,求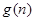 的最大值;
的最大值;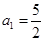 ,数列
,数列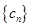 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.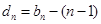 ,
,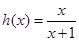 .
.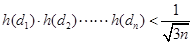 .
. 中
中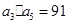 ,
, ,求
,求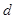 ;
; .
.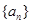 的前n项和为
的前n项和为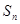 ,且满足:
,且满足: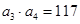 ,
,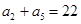 .
.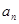 ;
;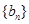 是等差数列,且
是等差数列,且 ,求非零常数c;
,求非零常数c;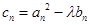 ,已知数列
,已知数列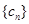 为递增数列,求实数
为递增数列,求实数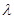 的取值范围.
的取值范围. 的公差
的公差 ,等比数列
,等比数列 为公比为
为公比为 ,且
,且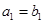 ,
, ,
, .
. ,是否存在正整数
,是否存在正整数 (其中
(其中 )使得
)使得 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组 满足:
满足: ,
, ,
,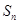 .
. 及
及 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
.