题目内容
19.在△ABC中,角A、B、C所对的边分别为a、b、c,若c=$\sqrt{3},b=1,B={30°}$,则△ABC的面积为$\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$.分析 根据题意和正弦定理求出sinC的值,由内角的范围求出角C,再由内角和定理分别求出角A和△ABC的面积.
解答 解:∵c=$\sqrt{3},b=1,B={30°}$,
∴由正弦定理得,$\frac{b}{sinB}=\frac{c}{sinC}$,则sinC=$\frac{csinB}{b}$=$\frac{\sqrt{3}×\frac{1}{2}}{1}$=$\frac{\sqrt{3}}{2}$,
由0<C<π得,C=60°或120°,
①当C=60°时,A=180°-B-C=90°,
∴△ABC的面积S=$\frac{1}{2}bc$=$\frac{\sqrt{3}}{2}$;
②当C=120°时,A=180°-B-C=30°,
∴△ABC的面积S=$\frac{1}{2}bcsinA$=$\frac{\sqrt{3}}{4}$,
综上可得,△ABC的面积是$\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$,
故答案为:$\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$.
点评 本题考查正弦定理,内角和定理的应用,注意内角的范围,考查分类讨论思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知{an}是等比数列,有a3•a11=4a7,{bn}是等差数列,且a7=b7,则b5+b9=( )
| A. | 4 | B. | 8 | C. | 0或8 | D. | 16 |
7.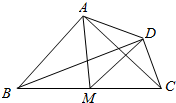 如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
 如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )| A. | 1 | B. | -1 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
14.若点P是曲线y=x2-lnx上任意一点,则点P到直线y=x+3的最小距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{3}$ |
4.设复数z的共轭复数是$\overline{z}$,z=3+i,则$\frac{1}{\overline{z}}$等于( )
| A. | 3+i | B. | 3-i | C. | $\frac{3}{10}$i+$\frac{1}{10}$ | D. | $\frac{3}{10}$+$\frac{1}{10}$i |