题目内容
9.设函数$f(x)={x^3}-\frac{1}{2}{x^2}-2x+5$,若对于任意x∈[-1,2]都有f(x)<m成立,求实数m的取值范围.分析 求导f′(x)=3x2-x-2=(3x+2)(x-1),从而可判断出f(x)在[-1,-$\frac{2}{3}$),(1,2]上单调递增,在(-$\frac{2}{3}$,1)上单调递减;从而求得fmax(x)=f(2)=7;从而解得.
解答 解:∵$f(x)={x^3}-\frac{1}{2}{x^2}-2x+5$,
∴f′(x)=3x2-x-2=(3x+2)(x-1),
∴当x∈[-1,-$\frac{2}{3}$),(1,2]时,f′(x)>0;
当x∈(-$\frac{2}{3}$,1)时,f′(x)<0;
∴f(x)在[-1,-$\frac{2}{3}$),(1,2]上单调递增,在(-$\frac{2}{3}$,1)上单调递减;
且f(-$\frac{2}{3}$)=-$\frac{8}{27}$-$\frac{1}{2}$×$\frac{4}{9}$+2×$\frac{2}{3}$+5=5+$\frac{22}{27}$,f(2)=8-$\frac{1}{2}$×4-2×2+5=7;
故fmax(x)=f(2)=7;
故对于任意x∈[-1,2]都有f(x)<m成立可化为7<m;
故实数m的取值范围为(7,+∞).
点评 本题考查了导数的综合应用及恒成立问题的处理方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.在区间(-1,1)上单调递增且为奇函数的是( )
| A. | y=ln(x+1) | B. | y=xsinx | C. | y=x-x3 | D. | y=3x+sinx |
19.点O是平行四边形ABCD的两条对角线的交点,则$\overrightarrow{AO}$+$\overrightarrow{OC}$+$\overrightarrow{CB}$等于( )
| A. | $\overrightarrow{AB}$ | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{CD}$ | D. | $\overrightarrow{DA}$ |
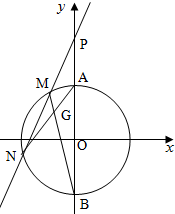 已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点.
已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点.