题目内容
13.定义一个集合A的所有子集组成的集合叫做集合A的幂集,记为P(A),用n(A)表示有限集A的元素个数.给出下列命题:①对于任意集合A,都有A∈P(A);
②存在集合A,使得n[P(A)]=3;
③若A∩B=∅,则P(A)∩P(B)=∅;
④若A⊆B,则P(A)⊆P(B);
⑤若n(A)-n(B)=1,则n[P(A)]=2×n[P(B)].
其中所有正确命题的序号为①④⑤.
分析 直接利用新定义判断五个命题的真假即可.
解答 解:由P(A)的定义可知①正确,④正确,
设n(A)=n,则n(P(A))=2n,∴②错误,
若A∩B=∅,则P(A)∩P(B)={∅},③不正确;
n(A)-n(B)=1,即A中元素比B中元素多1个,
则n[P(A)]=2×n[P(B)].⑤正确,
故答案为:①④⑤;
点评 本题考查集合的子集关系,集合的基本运算,新定义的理解与应用.

练习册系列答案
相关题目
3.平行四边形ABCD中,AC与BD交于点O,M为OC的中点,若$\overrightarrow{AB}$=(2,4),$\overrightarrow{AC}$=(1,3),则$\overrightarrow{AD}•\overrightarrow{BM}$等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 3 | D. | -3 |
18.任意连接长方体四个顶点构成的四面体,其最多可以有几个面是直角三角形( )
| A. | 一个 | B. | 两个 | C. | 三个 | D. | 四个 |
5.某种产品的广告费用支出X与销售额之间有如下的对应数据:
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为10销售收入y的值.
参考公式:最小二乘法得$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{{x}^{2}}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$其中:$\widehat{b}$是回归方程的斜率,$\widehat{a}$是截距.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)求回归直线方程;
(3)据此估计广告费用为10销售收入y的值.
参考公式:最小二乘法得$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{{x}^{2}}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$其中:$\widehat{b}$是回归方程的斜率,$\widehat{a}$是截距.
3.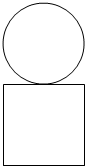 某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )
某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )
 某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )
某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )| A. | 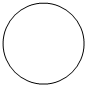 | B. |  | C. | 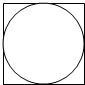 | D. |  |