题目内容
9.在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数f(x)的图象恰好通过n(n∈N*)个整点,则称函数f(x)为n阶整点函数.有下列函数:①f(x)=sin2x;
②g(x)=x3;
③h(x)=($\frac{1}{3}$)x;
④φ(x)=lnx.
其中是一阶整点函数有( ) 个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据新定义的“一阶整点函数”的要求,对于四个函数一一加以分析,它们的图象是否通过一个整点,从而选出答案即可.
解答 解:对于函数f(x)=sin2x,它只通过一个整点(0,0),故它是一阶整点函数;
对于函数g(x)=x3,当x∈Z时,一定有g(x)=x3∈Z,即函数g(x)=x3通过无数个整点,它不是一阶整点函数;
对于函数h(x)=($\frac{1}{3}$)x ,当x=0,-1,-2,时,h(x)都是整数,故函数h(x)通过无数个整点,它不是一阶整点函数;
对于函数φ(x)=lnx,它只通过一个整点(1,0),故它是一阶整点函数.
故选:B.
点评 本小题主要考查函数模型的选择与应用,属于基础题,解决本题的关键是对于新定义的概念的理解,即什么叫做:“一阶整点函数”,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
20.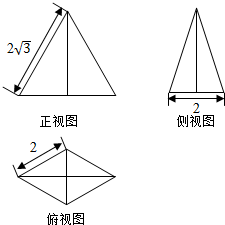 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 4$\sqrt{3}$ | D. | 2 |
17.直线l经过点(1,2),且倾斜角是直线y=x倾斜角的2倍,则以下各点在直线l上的是( )
| A. | (1,1) | B. | (2,2) | C. | (2,1) | D. | (2,0) |
14.设数列是{an}(n∈N*)是等差数列,若a1+a5=4,则a3=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
1.已知集合$A=(-∞,\frac{1}{2}]$,函数y=ln(2x+1)的定义域为集合B,则A∩B=( )
| A. | $({-\frac{1}{2},\frac{1}{2}}]$ | B. | $({-\frac{1}{2},\frac{1}{2}})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $[{\frac{1}{2},+∞})$ |
18.若集合A={(x,y)||x-1|+$\sqrt{y-4}$=0},B={1,4},则下面选项正确的是( )
| A. | B⊆A | B. | A⊆B | C. | A=B | D. | A∩B=Φ |
19.已知角α的终边上有一点P(1,-1),则cosα=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | 1 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{2}}{2}$ |