题目内容
(本小题满分16分)
对于函数y=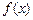 ,x∈(0,
,x∈(0, ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么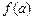 ,
,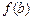 ,
,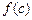 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数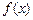 为“保三角形函数”.
为“保三角形函数”.
对于函数y= ,x∈
,x∈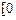 ,
, ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有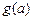 ,
,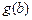 ,
,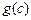 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数 为“恒三角形函数”.
为“恒三角形函数”.
(1)判断三个函数“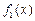 =x,
=x, =
=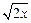 ,
,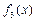 =
=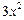 (定义域均为x∈(0,
(定义域均为x∈(0, )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由;
(2)若函数 =
=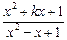 ,x∈
,x∈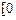 ,
, 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围;
(3)如果函数 是定义在(0,
是定义在(0, 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0, ,试证明:
,试证明: 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.
对于函数y=
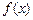 ,x∈(0,
,x∈(0, ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么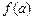 ,
,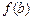 ,
,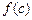 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数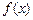 为“保三角形函数”.
为“保三角形函数”.对于函数y=
 ,x∈
,x∈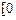 ,
, ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有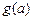 ,
,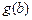 ,
,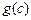 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数 为“恒三角形函数”.
为“恒三角形函数”.(1)判断三个函数“
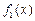 =x,
=x, =
=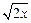 ,
,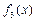 =
=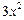 (定义域均为x∈(0,
(定义域均为x∈(0, )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由;(2)若函数
 =
=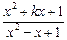 ,x∈
,x∈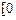 ,
, 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围;(3)如果函数
 是定义在(0,
是定义在(0, 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0, ,试证明:
,试证明: 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.解析:(1)对于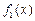 =x,它在(0,
=x,它在(0, 上是增函数,不妨设a≤b≤c,则
上是增函数,不妨设a≤b≤c,则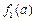 ≤
≤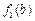 ≤
≤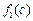 ,因为a+b>c,所以
,因为a+b>c,所以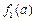 +
+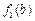 =a+b>c=
=a+b>c=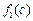 ,故
,故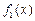 是“保三角形函数”.
是“保三角形函数”.
对于 =
=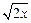 ,它在(0,
,它在(0, 上是增函数,,不妨设a≤b≤c,则
上是增函数,,不妨设a≤b≤c,则 ≤
≤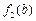 ≤
≤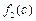 ,因为a+b>c,所以
,因为a+b>c,所以 +
+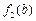 =
=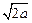 +
+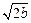 =
=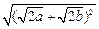 >
>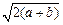 >
>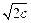 =
=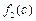 ,故
,故 是“保三角形函数”.
是“保三角形函数”.
对于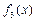 =
=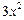 ,取a=3,b=3,c=5,显然a,b,c是一个三角形的三边长,但因为
,取a=3,b=3,c=5,显然a,b,c是一个三角形的三边长,但因为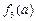 +
+ =
=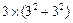 <
<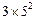 =
=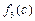 ,所以
,所以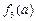 ,
, ,
,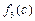 不是三角形的三边长,故
不是三角形的三边长,故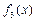 不是“保三角形函数”.
不是“保三角形函数”.
(2)解法1:因为 =1+
=1+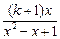 ,所以当x=0时,
,所以当x=0时, =1;当x>0时,
=1;当x>0时, =1+
=1+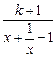 .
.
①当k=-1时,因为 =1,适合题意.
=1,适合题意.
②当k>-1时,因为 =1+
=1+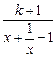 ≤1+
≤1+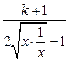 =k+2,所以
=k+2,所以 ∈
∈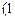 ,
,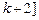 .从而当k>
.从而当k>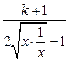 -1时,
-1时, ∈
∈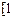 ,
,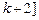 .由1+1>k+2,得k<0,所以-1<k<0.
.由1+1>k+2,得k<0,所以-1<k<0.
③当k<-1时,因为 =1+
=1+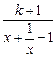 ≥1+
≥1+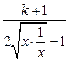 =k+2,所以
=k+2,所以 ∈
∈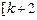 ,
,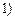 ,从而当k>-1时,所以
,从而当k>-1时,所以 ∈
∈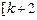 ,
, .由
.由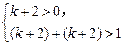 得,k>
得,k>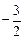 ,所以
,所以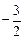 <k<-1.
<k<-1.
综上所述,所求k的取值范围是(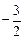 ,0).
,0).
解法2:因为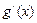 =
=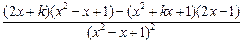 =
=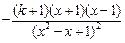 ,
,
①当k=-1时,因为 =1,适合题意.
=1,适合题意.
②当k>-1时,可知 在
在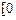 ,
,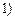 上单调递增,在
上单调递增,在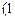 ,
, 上单调递减,而
上单调递减,而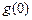 =1,
=1, =k+2,且当x>1时,
=k+2,且当x>1时, >1,所以此时
>1,所以此时 ∈
∈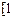 ,
,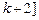 .
.
③当k<-1时,可知 在
在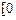 ,
,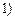 上单调递减,在
上单调递减,在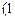 ,
, 上单调递增,而
上单调递增,而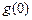 =1,
=1, =k+2,且当x>1时,
=k+2,且当x>1时, <1,所以此时
<1,所以此时 ∈
∈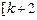 ,
, .
.
(以下同解法1)
(3)①因为 的值域是(0,
的值域是(0, ,所以存在正实数a,b,c,使得
,所以存在正实数a,b,c,使得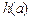 =1,
=1,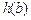 =1,
=1,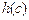 =2,显然这样的
=2,显然这样的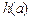 ,
,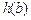 ,
,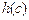 不是一个三角形的三边长.
不是一个三角形的三边长.
故 不是“恒三角形函数”.
不是“恒三角形函数”.
②因为 的最小正周期为T(T>0),令a=b=m+kT,c=n,其中k∈
的最小正周期为T(T>0),令a=b=m+kT,c=n,其中k∈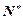 ,且k>
,且k>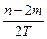 ,则a+b>c,又显然b+c>a,c+a>b,所以a,b,c是一个三角形的三边长.
,则a+b>c,又显然b+c>a,c+a>b,所以a,b,c是一个三角形的三边长.
但因为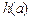 =
=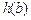 =
=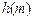 =1,
=1,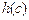 =
=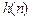 =2,所以
=2,所以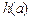 ,
,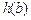 ,
,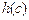 不是一个三角形的三边长.
不是一个三角形的三边长.
故 也不是“保三角形函数”.
也不是“保三角形函数”.
(说明:也可以先证 不是“保三角形函数”,然后根据此知
不是“保三角形函数”,然后根据此知 也不是“恒三角形函数”.)
也不是“恒三角形函数”.)
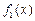 =x,它在(0,
=x,它在(0, 上是增函数,不妨设a≤b≤c,则
上是增函数,不妨设a≤b≤c,则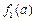 ≤
≤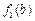 ≤
≤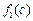 ,因为a+b>c,所以
,因为a+b>c,所以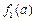 +
+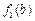 =a+b>c=
=a+b>c=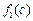 ,故
,故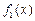 是“保三角形函数”.
是“保三角形函数”.对于
 =
=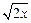 ,它在(0,
,它在(0, 上是增函数,,不妨设a≤b≤c,则
上是增函数,,不妨设a≤b≤c,则 ≤
≤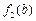 ≤
≤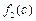 ,因为a+b>c,所以
,因为a+b>c,所以 +
+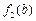 =
=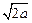 +
+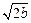 =
=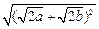 >
>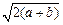 >
>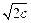 =
=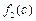 ,故
,故 是“保三角形函数”.
是“保三角形函数”.对于
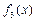 =
=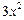 ,取a=3,b=3,c=5,显然a,b,c是一个三角形的三边长,但因为
,取a=3,b=3,c=5,显然a,b,c是一个三角形的三边长,但因为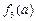 +
+ =
=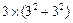 <
<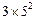 =
=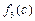 ,所以
,所以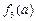 ,
, ,
,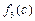 不是三角形的三边长,故
不是三角形的三边长,故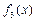 不是“保三角形函数”.
不是“保三角形函数”.(2)解法1:因为
 =1+
=1+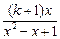 ,所以当x=0时,
,所以当x=0时, =1;当x>0时,
=1;当x>0时, =1+
=1+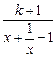 .
.①当k=-1时,因为
 =1,适合题意.
=1,适合题意.②当k>-1时,因为
 =1+
=1+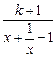 ≤1+
≤1+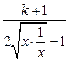 =k+2,所以
=k+2,所以 ∈
∈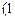 ,
,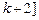 .从而当k>
.从而当k>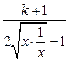 -1时,
-1时, ∈
∈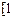 ,
,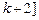 .由1+1>k+2,得k<0,所以-1<k<0.
.由1+1>k+2,得k<0,所以-1<k<0.③当k<-1时,因为
 =1+
=1+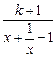 ≥1+
≥1+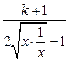 =k+2,所以
=k+2,所以 ∈
∈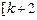 ,
,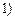 ,从而当k>-1时,所以
,从而当k>-1时,所以 ∈
∈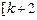 ,
, .由
.由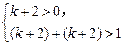 得,k>
得,k>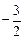 ,所以
,所以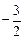 <k<-1.
<k<-1.综上所述,所求k的取值范围是(
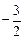 ,0).
,0).解法2:因为
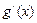 =
=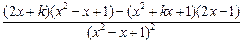 =
=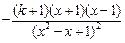 ,
,①当k=-1时,因为
 =1,适合题意.
=1,适合题意.②当k>-1时,可知
 在
在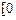 ,
,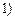 上单调递增,在
上单调递增,在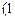 ,
, 上单调递减,而
上单调递减,而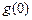 =1,
=1, =k+2,且当x>1时,
=k+2,且当x>1时, >1,所以此时
>1,所以此时 ∈
∈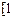 ,
,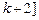 .
.③当k<-1时,可知
 在
在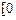 ,
,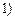 上单调递减,在
上单调递减,在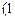 ,
, 上单调递增,而
上单调递增,而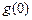 =1,
=1, =k+2,且当x>1时,
=k+2,且当x>1时, <1,所以此时
<1,所以此时 ∈
∈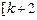 ,
, .
.(以下同解法1)
(3)①因为
 的值域是(0,
的值域是(0, ,所以存在正实数a,b,c,使得
,所以存在正实数a,b,c,使得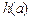 =1,
=1,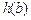 =1,
=1,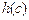 =2,显然这样的
=2,显然这样的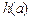 ,
,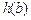 ,
,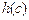 不是一个三角形的三边长.
不是一个三角形的三边长.故
 不是“恒三角形函数”.
不是“恒三角形函数”.②因为
 的最小正周期为T(T>0),令a=b=m+kT,c=n,其中k∈
的最小正周期为T(T>0),令a=b=m+kT,c=n,其中k∈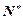 ,且k>
,且k>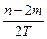 ,则a+b>c,又显然b+c>a,c+a>b,所以a,b,c是一个三角形的三边长.
,则a+b>c,又显然b+c>a,c+a>b,所以a,b,c是一个三角形的三边长.但因为
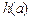 =
=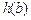 =
=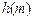 =1,
=1,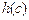 =
=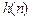 =2,所以
=2,所以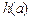 ,
,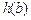 ,
,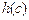 不是一个三角形的三边长.
不是一个三角形的三边长.故
 也不是“保三角形函数”.
也不是“保三角形函数”.(说明:也可以先证
 不是“保三角形函数”,然后根据此知
不是“保三角形函数”,然后根据此知 也不是“恒三角形函数”.)
也不是“恒三角形函数”.)略

练习册系列答案
相关题目
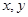 ,定义运算“
,定义运算“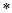 ”,
”,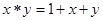 .若点
.若点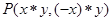 在第四象限,点
在第四象限,点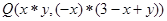 在第一象限,当
在第一象限,当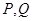 变动时动点
变动时动点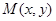 形成的平面区域为
形成的平面区域为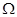 ,则使
,则使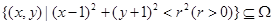 成立的
成立的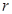 的最大值为
的最大值为 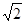
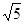
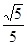
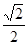
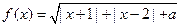 .
.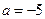 时,求函数
时,求函数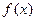 的定义域;
的定义域;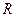 ,试求实数
,试求实数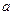 的取值范围.
的取值范围.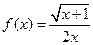 的定义域是 .
的定义域是 .
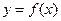 的导函数图象经过点
的导函数图象经过点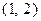 ,则
,则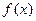 的解析式为( )
的解析式为( )
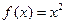


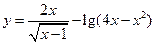 的定义域是:
的定义域是: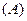
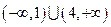
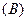
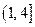
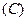
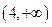

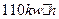 B.
B.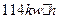 C.
C.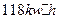 D.
D.