题目内容
某市原来居民用电价为0.52元/kw·h,换装分时电表后,峰时段(早上八点到晚上九点)的电价0.55元/kw·h ,谷时段(晚上九点到次日早上八点)的电价为0.35元/kw·h.对于一个平均每月用电量为200kw·h 的家庭,换装分时电表后,每月节省的电费不少于原来电费的10%,则这个家庭每月在峰时段的平均用电量至多为 ( )
A.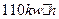 B.
B.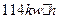 C.
C.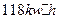 D.
D.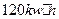
A.
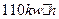 B.
B.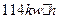 C.
C.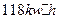 D.
D.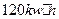
C
略

练习册系列答案
相关题目
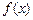 ,x∈(0,
,x∈(0, ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么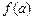 ,
,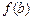 ,
,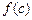 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数 ,x∈
,x∈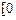 ,
,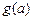 ,
,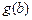 ,
,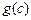 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数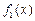 =x,
=x, =
=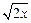 ,
,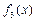 =
=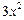 (定义域均为x∈(0,
(定义域均为x∈(0,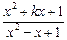 ,x∈
,x∈ 是定义在(0,
是定义在(0,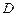 的函数
的函数 ,若有常数M,使得对任意的
,若有常数M,使得对任意的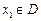 ,存在唯一的
,存在唯一的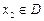 满足等式
满足等式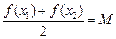 ,则称M为函数
,则称M为函数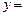 f (x)的“均值”.
f (x)的“均值”.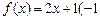 ≤
≤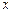 ≤
≤ 的“均值”,请说明理由;
的“均值”,请说明理由;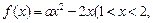
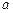 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围; 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数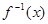 是函数
是函数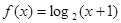 的反函数,若
的反函数,若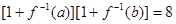 ,则f(a+b)的值为
,则f(a+b)的值为 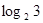
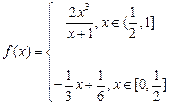 ,函数
,函数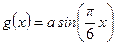
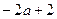 (a>0),若存在
(a>0),若存在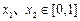 ,使得
,使得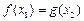 成立,则实数
成立,则实数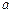 的取值范围是( )
的取值范围是( )
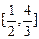
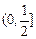
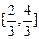
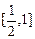
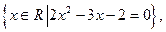 用列举法表示为____________.
用列举法表示为____________.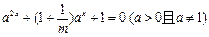 有解,则m的取值范围是
有解,则m的取值范围是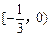
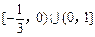
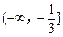
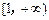
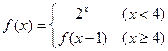 , 则
, 则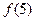 _____________.
_____________.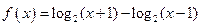 .
.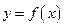 的奇偶性;
的奇偶性;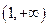 上增减性,并进行证明;
上增减性,并进行证明;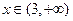 时,不等式
时,不等式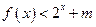 恒成立,求实数
恒成立,求实数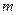 的取值范围.
的取值范围.