题目内容
20.已知曲线C的方程kx2-(4-k)y2=k-1(1)若曲线C是双曲线,且一条渐进线是y=$\sqrt{3}$x求双曲线方程;
(2)当k=-2时,在曲线C上是否存在关于直线l:y=x+m对称的两P(x1,y1),Q(x2,y2)若存在求m的取值范围,若不存在说明理由.
分析 (1)当k=0或k=1或k=4时,C表示直线;当k≠0且k≠-1且k≠4时方程为$\frac{{x}^{2}}{\frac{k-1}{k}}-\frac{{y}^{2}}{\frac{k-1}{4-k}}=1$,由此能求出曲线C是双曲线,且一条渐进线是y=$\sqrt{3}$x的双曲线方程;
(2)当k=-2时,曲线C的方程为$\frac{2{x}^{2}}{3}+2{y}^{2}=1$.设曲线C上存在关于直线l:y=x+m对称的两P(x1,y1),Q(x2,y2),再设P、Q的中点是M(x0,y0),由点差法结合PQ中点M在直线l上求出M的坐标,再由点M在椭圆内部求得m的取值范围.
解答 解:(1)当k=0或k=4或k=1时,C表示直线;
当k≠0且k≠1且k≠4时方程为$\frac{{x}^{2}}{\frac{k-1}{k}}-\frac{{y}^{2}}{\frac{k-1}{4-k}}=1$,①
方程①表示双曲线,且一条渐进线是y=$\sqrt{3}$x,
则$\left\{\begin{array}{l}{\frac{k-1}{k}>0}\\{\frac{k-1}{4-k}>0}\\{\frac{k}{4-k}=3}\end{array}\right.$或$\left\{\begin{array}{l}{\frac{k-1}{4-k}<0}\\{\frac{k-1}{k}<0}\\{\frac{k}{4-k}=3}\end{array}\right.$.
解得:k=3.
∴双曲线方程为$\frac{3{x}^{2}}{2}-\frac{{y}^{2}}{2}=1$;
(2)当k=-2时,曲线C的方程为$\frac{2{x}^{2}}{3}+2{y}^{2}=1$.
设曲线C上存在关于直线l:y=x+m对称的两P(x1,y1),Q(x2,y2).
再设P、Q的中点是M(x0,y0),
则$\frac{2{{x}_{1}}^{2}}{3}+2{{y}_{1}}^{2}=1$,$\frac{2{{x}_{2}}^{2}}{3}+2{{y}_{2}}^{2}=1$,
两式作差可得x0=3y0,
又M(x0,y0)在直线l上,∴y0=x0+m,
联立$\left\{\begin{array}{l}{{x}_{0}=3{y}_{0}}\\{{y}_{0}={x}_{0}+m}\end{array}\right.$,解得M($-\frac{3m}{2},-\frac{m}{2}$),
由M在椭圆$\frac{2{x}^{2}}{3}+2{y}^{2}=1$内部.
可得$\frac{2(-\frac{3m}{2})^{2}}{3}+2(-\frac{m}{2})^{2}<1$,
解得:-$\frac{\sqrt{2}}{2}<m<\frac{\sqrt{2}}{2}$.
∴曲线C上是存在关于直线l:y=x+m对称的两P(x1,y1),Q(x2,y2),
此时m的取值范围是($-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}$).
点评 本题考查直线与圆锥曲线的综合运用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.

| A. | 不能作出这样的三角形 | B. | 能作出一个锐角三角形 | ||
| C. | 能作出一个直角三角形 | D. | 能作出一个钝角三角形 |
| A. | 负角一定在第四象限 | B. | 钝角比第三象限的角小 | ||
| C. | 坐标轴上的角都是正角 | D. | 锐角都是第一象限的角 |
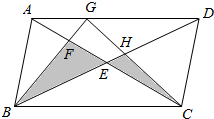 如图,长方形ABCD的面积为96cm2,四边形EFGH的面积为7.5cm2,那么阴影部分的面积是多少?
如图,长方形ABCD的面积为96cm2,四边形EFGH的面积为7.5cm2,那么阴影部分的面积是多少?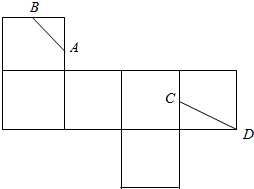 如图是一个正方体的平面展开图,A,B,C均为所在棱的中点,D为正方体的顶点,若正方体的棱长为2,则在正方体中,封闭折线ABCDA的长为3$\sqrt{2}+\sqrt{5}$.
如图是一个正方体的平面展开图,A,B,C均为所在棱的中点,D为正方体的顶点,若正方体的棱长为2,则在正方体中,封闭折线ABCDA的长为3$\sqrt{2}+\sqrt{5}$.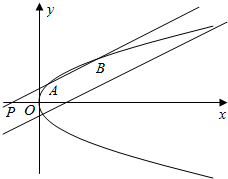 如图,已知抛物线C:y2=4x,点P(a,0),其中a<0,过点P作直线l1:x=my+a,与C交于不同的两点A,B
如图,已知抛物线C:y2=4x,点P(a,0),其中a<0,过点P作直线l1:x=my+a,与C交于不同的两点A,B