题目内容
11.极坐标系中,和点(3,$\frac{π}{6}$)表示同一点的是(3,2kπ+$\frac{π}{6}$),k∈Z.分析 因为(ρ,θ),(ρ,θ+2kπ)(k∈Z)表示极坐标系中同一点,据此可得答案.
解答 解:∵ρ=3,θ=$\frac{π}{6}$=2kπ+$\frac{π}{6}$,k∈Z,
∴点(3,2kπ+$\frac{π}{6}$),k∈Z与(3,$\frac{π}{6}$)表示极坐标系中同一点.
故答案为:(3,2kπ+$\frac{π}{6}$),k∈Z
点评 本题考查了极坐标系中表示同一点的坐标问题,理解(ρ,θ),(ρ,θ+2kπ)(k∈Z)表示极坐标系中同一点是解决问题的关键.

练习册系列答案
相关题目
19.已知函数f(x)=2cosx(sinx+cosx),则下列说法正确的是( )
| A. | f(x)的最小正周期为2π | |
| B. | f(x)的图象关于点$(-\frac{π}{8},0)$对称 | |
| C. | f(x)的图象关于直线$x=\frac{π}{8}$对称 | |
| D. | f(x)的图象向左平移$\frac{π}{4}$个单位长度后得到一个偶函数图象 |
3.已知函数f(x)=ax2-2ax+c满足f(2013)<f(-2012),则满足f(m)≤f(0)的实数m的取值范围是( )
| A. | (-∞,0] | B. | [2,+∞) | C. | (-∞,0]∪[2,+∞) | D. | [0,2] |
1.点M是抛物线y=$\frac{1}{4}$x2上一点,F为抛物线的焦点,以MF为直径的圆与x轴的位置关系为( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |

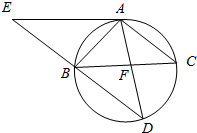 如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5.
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=6,BD=5.