题目内容
5.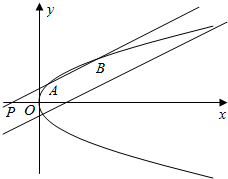 如图,已知抛物线C:y2=4x,点P(a,0),其中a<0,过点P作直线l1:x=my+a,与C交于不同的两点A,B
如图,已知抛物线C:y2=4x,点P(a,0),其中a<0,过点P作直线l1:x=my+a,与C交于不同的两点A,B(1)若a=-2,求实数m的取值范围
(2)记直线l2:x=my-a,以线段AB为其中一边作一矩形,且另一边在直线l2上,若该矩形的面积记为S,点P与线段AB中点的距离记为d,求$\frac{d}{S}$的取值范围.
分析 (1)直线方程与抛物线方程联立,利用判别式,即可求实数m的取值范围;
(2)直线l1:x=my+a代入抛物线C:y2=4x,求出|AB|,d,表示出$\frac{d}{S}$,换元,利用基本不等式,即可求$\frac{d}{S}$的取值范围.
解答 解:(1)若a=-2,则直线l1:x=my-2,
代入抛物线C:y2=4x,整理可得y2-4my+8=0,
∴△=16m2-32>0,
∴m<-$\sqrt{2}$或m$>\sqrt{2}$;
(2)直线l1:x=my+a代入抛物线C:y2=4x,整理可得y2-4my-4a=0,
∴△=16m2+16a>0,
设A(x1,y1),B(x2,y2).则y1+y2=4m,y1y2=-4a
∴x1+x2=m(y1+y2)+2a=4m2+2a,x1x2=a2,
设线段AB的中点为Q,则Q(2m2+a,2m),
∴d=$\sqrt{[a-(2{m}^{2}+a)]^{2}+(0-2m)^{2}}$=|2m|•m$\sqrt{{m}^{2}+1}$,|AB|=4$\sqrt{({m}^{2}+1)({m}^{2}+a)}$.
∵直线l1与l2的距离=$\frac{|2a|}{\sqrt{{m}^{2}+1}}$,
∴S=|AB|•$\frac{|2a|}{\sqrt{{m}^{2}+1}}$=8|a|$\sqrt{{m}^{2}+a}$,
∴$\frac{d}{S}$=$\frac{1}{4|a|}$•$\sqrt{\frac{{m}^{2}({m}^{2}+1)}{{m}^{2}+a}}$,
令m2+a=t(t>0),∴m2=t-a,
∴$\frac{d}{S}$=$\frac{1}{4|a|}\sqrt{t+\frac{(a-1)a}{t}+1-2a}$,
∵a<0,
∴(a-1)a>0,
∴$\frac{d}{S}$=$\frac{1}{4|a|}\sqrt{t+\frac{(a-1)a}{t}+1-2a}$≥-$\frac{1}{4a}\sqrt{2\sqrt{(a-1)a}+1-2a}$,
当且仅当t=$\sqrt{(a-1)a}$时,等号处理,
∴$\frac{d}{S}$的取值范围是[-$\frac{1}{4a}\sqrt{2\sqrt{(a-1)a}+1-2a}$,+∞).
点评 本题考查直线与抛物线的位置关系,考查矩形的面积,考查基本不等式的运用,正确转化是关键.

| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$或$\frac{3}{2}$ | D. | 1 |
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | x+2y=1=0 | B. | 2x-y-1=0 | C. | y=x | D. | y=1 |