题目内容
10. 如图,已知A(x1,y1)为抛物线y2=2px(p>0)上的动点,P(p,0)为定点.
如图,已知A(x1,y1)为抛物线y2=2px(p>0)上的动点,P(p,0)为定点.(1)过AP的中点M作x轴的平行线分别交抛物线及其准线于Q,N,试用x1表示点Q的横坐标xQ;
(2)求证:Q为MN的中点;
(3)以MN为直径的圆是否恒过一个定点?若存在,求出定点的坐标;若不存在,请说明理由.
分析 (1)通过中点坐标公式可知M($\frac{{x}_{1}+p}{2}$,$\frac{{y}_{1}}{2}$),利用M、Q的纵坐标相同计算即得结论;
(2)只需证明$\frac{{x}_{N}+{x}_{M}}{2}$=xQ即可,计算即得结论;
(3)通过抛物线的定义可知|QF|=|QN|,结合Q为MN的中点即得结论.
解答 (1)解:∵A(x1,y1)、P(p,0),
∴M($\frac{{x}_{1}+p}{2}$,$\frac{{y}_{1}}{2}$),
∵M、Q的纵坐标相同,
∴Q的横坐标满足:$\frac{{{y}_{1}}^{2}}{4}$=2pxQ,
又∵${{y}_{1}}^{2}$=2px1,
∴xQ=$\frac{{x}_{1}}{4}$;
(2)证明:∵N的横坐标xN=-$\frac{p}{2}$,
∴$\frac{{x}_{N}+{x}_{M}}{2}$=$\frac{-\frac{p}{2}+\frac{{x}_{1}+p}{2}}{2}$=$\frac{{x}_{1}}{4}$=xQ,
∴Q为MN的中点;
(3)结论:以MN为直径的圆恒过焦点F($\frac{p}{2}$,0).
理由如下:
由抛物线的定义可知:|QF|=|QN|,
又∵Q为MN的中点,
∴|QF|=$\frac{1}{2}$|MN|,
∴以MN为直径的圆恒过焦点F($\frac{p}{2}$,0).
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
20.若如图所示的程序框图运行后,输出的S的值为31,则判断框内填入的条件可以为( )
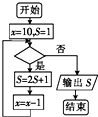

| A. | x>7? | B. | x>6? | C. | x≥6? | D. | x≤6? |
19.设l是直线,a,β是两个不同的平面,则下列正确的是( )
| A. | 若l∥a,l∥β,则a∥β | B. | 若α⊥β,l∥α,则l⊥β | C. | 若α⊥β,l⊥α,则l⊥β | D. | 若l∥α,l⊥β,则α⊥β |
