题目内容
20. 某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
附:线性回归方程:$\stackrel{∧}{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\overline{xy}-\overline{x}\overline{y}}{\overline{{x}^{2}}-{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
分析 (1)根据所给的数据,写出5组坐标,作出散点图如图所示.
(2)根据所给的数据先做出横标和纵标的平均数,利用最小二乘法写出线性回归方程系数的表达式,把样本中心点代入求出a的值,得到线性回归方程.
(3)根据所给的变量x的值,把值代入线性回归方程,得到对应的y的值,这里的y的值是一个预报值.
解答 解:(1)根据所给的数据,写出5组坐标,作出散点图如图所示: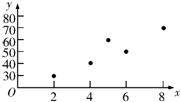 …(2分)
…(2分)
(2)求回归直线方程.
$\overline{x}$=$\frac{1}{5}$(2+4+5+6+8)=5,$\overline{y}$=$\frac{1}{5}$(30+40+60+50+70)=50…4分
$\sum _{i=1}^{5}$${x}_{i}^{2}$=145,
$\sum _{i=1}^{5}$xiyi=1380,…6 分
b=$\frac{\sum _{i=1}^{5}{x}_{i}{y}_{i}-5\overline{x}\overline{y}}{\sum _{i=1}^{5}{{x}_{i}}^{2}-5{\overline{x}}^{2}}$=$\frac{1380-5×5×50}{145-5×{5}^{2}}$=6.5,
a=50-6.5×5=17.5
∴因此回归直线方程为y=6.5x+17.5;…10分
(3)当x=12时,预报y的值为y=12×6.5+17.5=95.5万元.
即广告费用为12万元时,销售收入y的值大约是95.5万元.…(12分)
点评 本题考查线性回归方程的求法和应用,本题解题的关键是求出线性回归方程的系数,这是后面解题的先决条件.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),若以C的焦点F为圆心a为半径的圆,截双曲线的渐近线所得弦长为b,则此双曲线的离心率是( )
| A. | $\frac{3\sqrt{5}}{5}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
12.在△ABC中,a=3$\sqrt{3}$,b=2,cosC=$-\frac{{\sqrt{3}}}{2}$,则c等于( )
| A. | 13 | B. | $\sqrt{13}$ | C. | 7 | D. | 9 |
19.一台使用的时间较长的机器,按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
(1)如果y对x线性相关,且回归直线方程y=0.7286x-a,依据表中数据求a的值;
(2)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(精确到0.0001)
参考公式:$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.$.
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y件) | 11 | 9 | 8 | 5 |
(2)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(精确到0.0001)
参考公式:$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.$.