题目内容
已知向量a=(cosθ,sinθ),θ∈[0,π],向量b=( ,-1).
,-1).
(1)若a⊥b,求θ的值;
(2)若|2a-b|<m恒成立,求实数m的取值范围.
 ,-1).
,-1).(1)若a⊥b,求θ的值;
(2)若|2a-b|<m恒成立,求实数m的取值范围.
(1)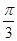 (2)(4,+∞)
(2)(4,+∞)
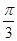 (2)(4,+∞)
(2)(4,+∞)解:(1)∵a⊥b,∴ cosθ-sinθ=0,得tanθ=
cosθ-sinθ=0,得tanθ= ,
,
又θ∈[0,π],∴θ=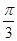 .
.
(2)∵2a-b=(2cosθ- ,2sinθ+1),
,2sinθ+1),
∴|2a-b|2=(2cosθ- )2+(2sinθ+1)2=8+8(
)2+(2sinθ+1)2=8+8(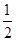 sinθ-
sinθ-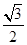 cosθ)=8+8sin(θ-
cosθ)=8+8sin(θ-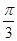 ),
),
又θ∈[0,π],∴θ-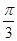 ∈[-
∈[-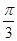 ,
,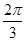 ],
],
∴sin(θ-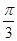 )∈[-
)∈[-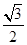 ,1],
,1],
∴|2a-b|2的最大值为16,
∴|2a-b|的最大值为4,
又|2a-b|<m恒成立,∴m>4.
故m的取值范围为(4,+∞).
 cosθ-sinθ=0,得tanθ=
cosθ-sinθ=0,得tanθ= ,
,又θ∈[0,π],∴θ=
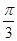 .
.(2)∵2a-b=(2cosθ-
 ,2sinθ+1),
,2sinθ+1),∴|2a-b|2=(2cosθ-
 )2+(2sinθ+1)2=8+8(
)2+(2sinθ+1)2=8+8(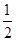 sinθ-
sinθ-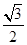 cosθ)=8+8sin(θ-
cosθ)=8+8sin(θ-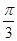 ),
),又θ∈[0,π],∴θ-
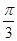 ∈[-
∈[-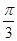 ,
,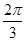 ],
],∴sin(θ-
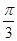 )∈[-
)∈[-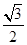 ,1],
,1],∴|2a-b|2的最大值为16,
∴|2a-b|的最大值为4,
又|2a-b|<m恒成立,∴m>4.
故m的取值范围为(4,+∞).

练习册系列答案
相关题目
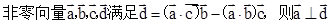
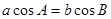 ,则△ABC是等腰三角形
,则△ABC是等腰三角形 中,
中,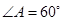 ,边长a,c分别为a=4,c=
,边长a,c分别为a=4,c=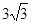 ,则
,则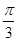 <θ≤π;
<θ≤π;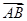 ·
·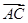 =0,
=0,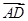 =0,
=0,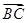 满足|
满足| 中,已知向量
中,已知向量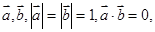 点
点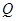 满足
满足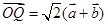 .曲线
.曲线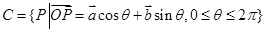 ,区域
,区域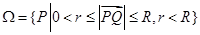 .若
.若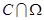 为两段分离的曲线,则( )
为两段分离的曲线,则( )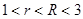
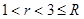
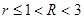
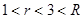
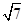 ,〈a,b〉=
,〈a,b〉=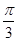 ,则|b|=( )
,则|b|=( )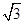
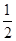 )∪(
)∪(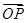 =
=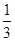 (
(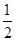
 +
+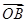 +2
+2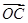 ),则点P一定为三角形ABC的( )
),则点P一定为三角形ABC的( )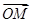 =ma,
=ma,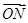 =nb,
=nb,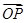 =αa+βb,其中m,n,α,β均为实数,m≠0,n≠0,若M、P、N三点共线,则
=αa+βb,其中m,n,α,β均为实数,m≠0,n≠0,若M、P、N三点共线,则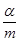 +
+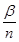 =________.
=________.