题目内容
下列命题中真命题的编号是________.(填上所有正确的编号)
①向量a与向量b共线,则存在实数λ使a=λb(λ∈R);
②a,b为单位向量,其夹角为θ,若|a-b|>1,则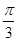 <θ≤π;
<θ≤π;
③A、B、C、D是空间不共面的四点,若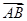 ·
·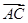 =0,
=0,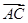 ·
·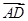 =0,
=0,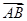 ·
·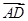 =0,则△BCD一定是锐角三角形;
=0,则△BCD一定是锐角三角形;
④向量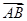 ,
,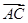 ,
,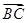 满足|
满足|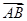 |=|
|=|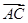 |+|
|+|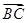 |,则
|,则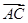 与
与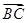 同向;
同向;
⑤若向量a∥b,b∥c,则a∥c.
①向量a与向量b共线,则存在实数λ使a=λb(λ∈R);
②a,b为单位向量,其夹角为θ,若|a-b|>1,则
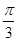 <θ≤π;
<θ≤π;③A、B、C、D是空间不共面的四点,若
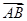 ·
·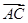 =0,
=0,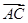 ·
·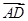 =0,
=0,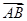 ·
·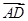 =0,则△BCD一定是锐角三角形;
=0,则△BCD一定是锐角三角形;④向量
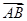 ,
,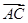 ,
,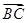 满足|
满足|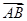 |=|
|=|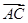 |+|
|+|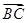 |,则
|,则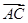 与
与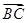 同向;
同向;⑤若向量a∥b,b∥c,则a∥c.
②③
①不是真命题,当b=0时,命题不成立;对于②,|a-b|=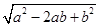 =
=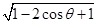 >1,解得cos θ<
>1,解得cos θ<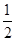 ,因为向量夹角范围是[0,π],所以θ∈
,因为向量夹角范围是[0,π],所以θ∈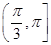 ;对于③,易知,BD>AB,CD>AC,所以BD2+CD2>AB2+AC2=BC2,所以∠BDC是锐角,同理可证其余两边所对的角都是锐角,所以△BCD一定是锐角三角形;④不对;当C点位于线段AB上时,满足题设条件,但是两向量是反向的;⑤不对,当b=0时,命题就不成立.
;对于③,易知,BD>AB,CD>AC,所以BD2+CD2>AB2+AC2=BC2,所以∠BDC是锐角,同理可证其余两边所对的角都是锐角,所以△BCD一定是锐角三角形;④不对;当C点位于线段AB上时,满足题设条件,但是两向量是反向的;⑤不对,当b=0时,命题就不成立.
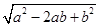 =
=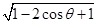 >1,解得cos θ<
>1,解得cos θ<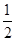 ,因为向量夹角范围是[0,π],所以θ∈
,因为向量夹角范围是[0,π],所以θ∈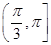 ;对于③,易知,BD>AB,CD>AC,所以BD2+CD2>AB2+AC2=BC2,所以∠BDC是锐角,同理可证其余两边所对的角都是锐角,所以△BCD一定是锐角三角形;④不对;当C点位于线段AB上时,满足题设条件,但是两向量是反向的;⑤不对,当b=0时,命题就不成立.
;对于③,易知,BD>AB,CD>AC,所以BD2+CD2>AB2+AC2=BC2,所以∠BDC是锐角,同理可证其余两边所对的角都是锐角,所以△BCD一定是锐角三角形;④不对;当C点位于线段AB上时,满足题设条件,但是两向量是反向的;⑤不对,当b=0时,命题就不成立.
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
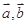 满足:
满足: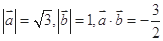 ,则向量
,则向量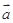 与
与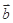 的夹角为( ).
的夹角为( ).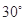
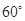
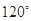

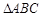 中,有如下四个命题:①
中,有如下四个命题:① ; ②
; ②
 ;③若
;③若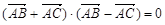 ,则
,则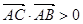 ,则
,则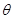 为两个非零向量
为两个非零向量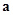 、
、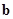 的夹角,已知对任意实数
的夹角,已知对任意实数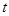 ,
,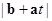 的最小值为1( )
的最小值为1( )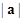 唯一确定
唯一确定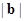 唯一确定
唯一确定 ,-1).
,-1).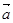 与
与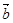 的夹角为
的夹角为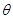 ,定义
,定义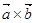 为
为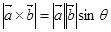 ,若
,若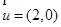 ,
,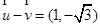 ,则
,则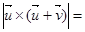 ( )
( )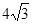 B.
B.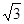
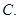
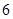
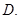
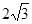
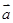 、
、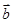 ,且
,且 =
= =
= 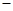 5
5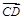 =7
=7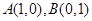 则与
则与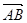 共线的单位向量为 .
共线的单位向量为 .