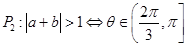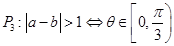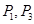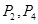题目内容
(2012·辽宁)已知两个非零向量a,b满足|a+b|=|a-b|,则下面结论正确的是( )
| A.a∥b | B.a⊥b |
| C.|a|=|b| | D.a+b=a-b |
B
将向量的模相等变为向量的平方相等求解.
因为|a+b|=|a-b|,
所以(a+b)2=(a-b)2,
即a·b=0,故a⊥b.
因为|a+b|=|a-b|,
所以(a+b)2=(a-b)2,
即a·b=0,故a⊥b.

练习册系列答案
相关题目
 ,-1).
,-1). ,则α和β的夹角θ的范围是 _________ .
,则α和β的夹角θ的范围是 _________ . ,1),B点是以原点O为圆心的单位圆上的动点,则|
,1),B点是以原点O为圆心的单位圆上的动点,则| +
+ |的最大值是( )
|的最大值是( )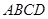 中,
中, ,点
,点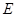 是
是 边的中点,点
边的中点,点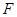 在边
在边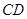 上.
上.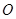 是对角线
是对角线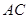 的中点,
的中点, 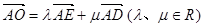 ,求
,求 的值;
的值;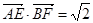 ,求线段
,求线段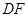 的长.
的长.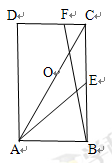
 是面积为4的
是面积为4的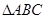 内部一点,且有
内部一点,且有 ,则
,则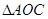 的面积为( )
的面积为( )
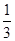
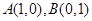 则与
则与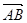 共线的单位向量为 .
共线的单位向量为 .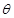 ,有下列四个命题
,有下列四个命题