题目内容
6.已知圆C的圆心在坐标原点,且被直线3x+4y+15=0截得的弦长为8(Ⅰ)试求圆C的方程;
(Ⅱ)当P在圆C上运动时,点D是P在x轴上的投影,M为线段PD上一点,且|MD|=$\frac{4}{5}$|PD|.求点M的轨迹方程.
分析 (Ⅰ)求出到直线3x+4y+15=0的距离,利用$8=2\sqrt{{r^2}-{d^2}}$,求出圆的半径,即可求出圆C的方程;
(Ⅱ)设点M的坐标是(x,y),P的坐标是(xP,yP),确定坐标之间的关系,利用P在圆x2+y2=25上,求点M的轨迹方程.
解答 解:(Ⅰ)已知圆C的圆心在坐标原点,且被直线3x+4y+15=0截得的弦长为8,
而圆心到直线3x+4y+15=0的距离d=3,
由弦长公式得$8=2\sqrt{{r^2}-{d^2}}$,所以r=5
所以所求圆的方程为x2+y2=25;(5分)
(Ⅱ)设点M的坐标是(x,y),P的坐标是(xP,yP),
∵点D是P在x轴上的投影,M为PD上一点,且|MD|=$\frac{4}{5}$|PD|,
∴xP=x,且yP=$\frac{5}{4}$y,∵P在圆x2+y2=25上,
∴x2+($\frac{5}{4}$y)2=25,整理得$\frac{x^2}{25}+\frac{y^2}{16}=1$,
即C的方程是$\frac{x^2}{25}+\frac{y^2}{16}=1$.(5分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查代入法求圆的方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.已知椭圆C的中心在原点,左焦点F1,右焦点F2均在x轴上,A为椭圆的右顶点,B为椭圆短轴的端点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,则此椭圆的离心率等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
1.对抛物线y=$\frac{1}{4}$x2,下列描述正确的是( )
| A. | 开口向上,焦点为(0,1) | B. | 开口向右,焦点为(1,0) | ||
| C. | 开口向上,焦点为(0,$\frac{1}{16}$) | D. | 开口向右,焦点为($\frac{1}{16}$,0) |
11.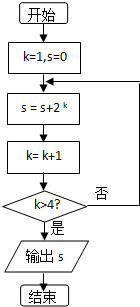 执行如图所示的程序框图,则输出s的值为( )
执行如图所示的程序框图,则输出s的值为( )
 执行如图所示的程序框图,则输出s的值为( )
执行如图所示的程序框图,则输出s的值为( )| A. | 30 | B. | 31 | C. | 62 | D. | 63 |
15.命题“关于x的不等式x2-ax+4>0在(0,+∞)上恒成立”的否定是( )
| A. | ?x∈(-∞,0),x2-ax+4>0 | B. | ?x∈(-∞,0),x2-ax+4>0 | ||
| C. | ?x∈(0,+∞),x2-ax+4≤0 | D. | ?x∈(0,+∞),x2-ax+4≤0 |