题目内容
1.对抛物线y=$\frac{1}{4}$x2,下列描述正确的是( )| A. | 开口向上,焦点为(0,1) | B. | 开口向右,焦点为(1,0) | ||
| C. | 开口向上,焦点为(0,$\frac{1}{16}$) | D. | 开口向右,焦点为($\frac{1}{16}$,0) |
分析 将抛物线方程化为标准方程,再由抛物线的性质,即可得到开口方向和焦点坐标.
解答 解:抛物线y=$\frac{1}{4}$x2,即为抛物线x2=4y,
由抛物线的性质可得该抛物线开口向上,
焦点为(0,1).
故选A.
点评 本题考查抛物线的方程和性质,主要考查抛物线的焦点,属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
9.$\int_0^1{({e^x}+2x)dx=}$( )
| A. | 1 | B. | e-1 | C. | e | D. | e+1 |
10.复数$\frac{i}{1+2i}$(i是虚数单位)的虚部是( )
| A. | $\frac{2}{5}$ | B. | -$\frac{2}{5}$ | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
 如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.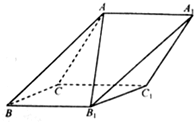 如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.
如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.