题目内容
12.AB是抛物线y=x2的一条弦,若AB的中点到x轴的距离为1,则弦AB的长度的最大值为$\frac{5}{2}$.分析 设A(x1,y1),B(x2,y2),则抛物线y=x2的准线方程为y=-$\frac{1}{4}$,利用抛物线的定义可得|AB|≤y1+y2+$\frac{1}{2}$,由弦AB的中点到x轴的距离是1,即可得出结论.
解答 解:设A(x1,y1),B(x2,y2),则抛物线y=x2的准线方程为y=-$\frac{1}{4}$,
∴|AB|≤y1+y2+$\frac{1}{2}$,
∵弦AB的中点到x轴的距离是1,
∴y1+y2=2,
∴|AB|≤$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 解决此类问题的关键是熟练掌握抛物线与直线的位置关系,正确运用抛物线的定义.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
2.下列函数中,为奇函数的是( )
| A. | y=2x+$\frac{1}{2^x}$ | B. | y=x,x∈(0,1] | C. | y=x3+x | D. | y=x3+1 |
3.函数f(x)=$\frac{{a}^{x+1}+{b}^{x+1}}{{a}^{x}+{b}^{x}}$(a>0,b>0,a≠b)在R上的单调性为( )
| A. | 增函数 | B. | 减函数 | C. | 不增不减函数 | D. | 与a,b的取值有关 |
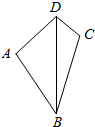 如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.
如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.