题目内容
【题目】某大型超市公司计划在![]() 市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中
市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中![]() 表示在该区开设分店的个数,
表示在该区开设分店的个数,![]() 表示这
表示这![]() 个分店的年收入之和):
个分店的年收入之和):
分店个数 | 2 | 3 | 4 | 5 | 6 |
年收入 | 250 | 300 | 400 | 450 | 600 |
(Ⅰ)该公司经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)假设该公司每年在新城区获得的总利润![]() (单位:万元)与
(单位:万元)与![]() ,
,![]() 之间的关系为
之间的关系为![]() ,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: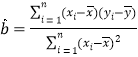
 ,
,![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)由题意结合回归方程系数的计算公式即可确定直线的回归方程;
(Ⅱ)结合(Ⅰ)的结论首先求得利润函数,然后结合均值不等式的结论即可确定利润取得最大值的分店个数和最大的利润值.
(Ⅰ)![]() ,
,![]() .
.
由公式:![]()
![]() ,
,
![]() ,
,
∴![]() ;
;
(Ⅱ)由题意:![]() ,
,
所以,年平均利润![]() ,
,
当且仅当![]() 时,取得等号,
时,取得等号,
所以,该公司在新城区开设4个分店时,新城区每年每个分店的平均利润最大为45万元.

【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、英语,为必考科目:“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、英语,为必考科目:“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生讲行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的
名学生讲行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有
列联表,请将列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
性别 | 选择物理 | 选择历史 | 总计 |
男生 | 50 | ||
女生 | 30 | ||
总计 |
(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
参考公式:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】随着生活水平的提高,人们的休闲方式也发生了变化.某机构随机调查了![]() 个人,其中男性占调查人数的
个人,其中男性占调查人数的![]() .已知男性中有一半的人的休闲方式是运动,而女性只有
.已知男性中有一半的人的休闲方式是运动,而女性只有![]() 人的休闲方式是运动.
人的休闲方式是运动.
(1)完成下列![]() 列联表:
列联表:
运动 | 非运动 | 总计 | |
男性 | |||
女性 | |||
总计 | n |
(2)若在犯错误的概率不超过![]() 的前提下,可认为“性别与休闲方式有关”, 那么本次被调查的人数至少有多少?
的前提下,可认为“性别与休闲方式有关”, 那么本次被调查的人数至少有多少?
(3)根据(2)的结论,本次被调查的人中,至少有多少人的休闲方式是运动?
参考公式![]() ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |