题目内容
【题目】如图,三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
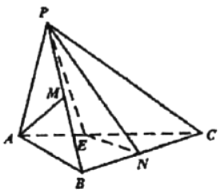
(1)求证:![]() 平面
平面![]() ;
;
(2)![]() 是线段
是线段![]() 上的点,且
上的点,且![]() 平面
平面![]() .
.
①确定点![]() 的位置;
的位置;
②求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)①![]() 为靠近
为靠近![]() 的
的![]() 的一个三等分点;②
的一个三等分点;②![]() .
.
【解析】
(1)由已知条件可证![]() ,即可证明结论;
,即可证明结论;
(2)①连结![]() ,交
,交![]() 于
于![]() ,则
,则![]() 是
是![]() 的重心,根据线面平行的性质定理,可证
的重心,根据线面平行的性质定理,可证![]() ,结合重心的性质,即可确定
,结合重心的性质,即可确定![]() 点位置;
点位置;
②作![]() 于
于![]() ,有
,有![]() ,从而有
,从而有![]() 平面
平面![]() ,得到
,得到![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,解直角
所成的角,解直角![]() ,即可得出结论.
,即可得出结论.
(1)![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() ,
,![]() 平面
平面![]() .
.
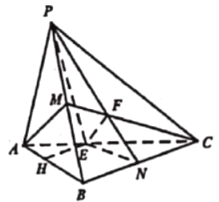
(2)①连结![]() ,交
,交![]() 于
于![]() ,则
,则![]() 是
是![]() 的重心,
的重心,
且![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,
即![]() 为靠近
为靠近![]() 的
的![]() 的一个三等分点.
的一个三等分点.
②作![]() 于
于![]() ,则
,则![]() ,
,![]() 平面
平面![]() ,
,
![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,
所成的角,
且![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】某大型超市公司计划在![]() 市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中
市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中![]() 表示在该区开设分店的个数,
表示在该区开设分店的个数,![]() 表示这
表示这![]() 个分店的年收入之和):
个分店的年收入之和):
分店个数 | 2 | 3 | 4 | 5 | 6 |
年收入 | 250 | 300 | 400 | 450 | 600 |
(Ⅰ)该公司经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)假设该公司每年在新城区获得的总利润![]() (单位:万元)与
(单位:万元)与![]() ,
,![]() 之间的关系为
之间的关系为![]() ,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: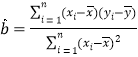
 ,
,![]() .
.